
【题目】如图,在ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB=![]() AC时,判断四边形EGCF是什么形状?请说明理由.
AC时,判断四边形EGCF是什么形状?请说明理由.
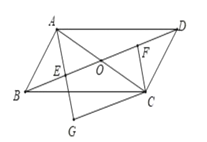
【答案】(1)证明见解析;(2)矩形,理由见解析.
【解析】
(1)根据题意由平行四边形的性质得出AB=CD,AB∥CD,OB=OD,OA=OC,由平行线的性质得出∠ABE=∠CDF,证出BE=DF,由SAS证明△ABE≌△CDF即可;
(2)由题意证出AB=OA,并由等腰三角形的性质得出AG⊥OB,∠OEG=90°,同理:CF⊥OD,得出EG∥CF,证出EG=CF,得出四边形EGCF是平行四边形,即可得出结论.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=![]() OB,DF=
OB,DF=![]() OD,
OD,
∴BE=DF,
在△ABE和△CDF中,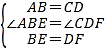 ,
,
∴△ABE≌△CDF(SAS).
(2)当AB=![]() AC时,四边形EGCF是矩形;理由如下:
AC时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
由(1)得:△ABE≌△CDF,
∴AE=CF,
∵EG=AE,
∴EG=CF,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
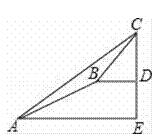
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及.
(1) 为获得东台市市民参与共享经济的活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同社区,选取部分市民进行问卷调查
(2) 调查小组随机调查了东台市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.
骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
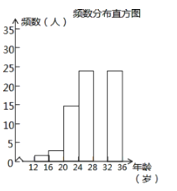
根据以上信息解答下列问题:
① 求出统计表中的a、b,并补全频数分布直方图;
② 试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2018年全国中学生数学竞赛情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下(部分未完成).请根据以上图表中提供的信息,解答下列问题:
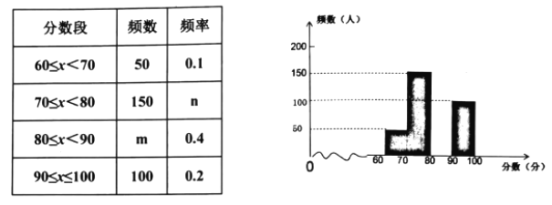
(1)本次调查的样本容量为______________.
(2)在表中:m=_____________,n=____________.
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,某中学有200人参加比赛,那么你估计该校约有多少人取得优秀成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九(1)班的2名男生1名女生、九(2)的1名男生1名女生共5人中选出2名主持人.
(1)用树形图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com