
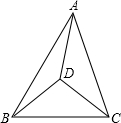
 如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,则∠ACB的度数为70度.
如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,则∠ACB的度数为70度. 分析 先根据等边对等角得:∠DAB=∠ABD,∠DBC=∠DCB,∠DAC=∠ACD,设∠DCA=x,∠DCB=y,
根据三角形的内角和列方程得:20+y+x+y+20+x=180,则x+y=70,所以∠ACB=70°.
解答 解:∵DA=DB=DC,
∴∠DAB=∠ABD,∠DBC=∠DCB,∠DAC=∠ACD,
设∠DCA=x,∠DCB=y,
∴∠ACB=x+y,
∵∠DAB=20°,
∴∠ABD=20°,
∵∠ABC+∠ACB+∠BAC=180°,
∴20+y+x+y+20+x=180,
x+y=70,
∴∠ACB=70°,
故答案为:70.
点评 本题考查了等腰三角形的性质,明确等边对等角是本题的关键,还利用了整体的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a5-a4bc是五次多项式 | |
| B. | 5m2n和-2nm2是同类项 | |
| C. | 如果两个数的绝对值相等,那么这两个数相等 | |
| D. | 3×102x2y是5次单项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
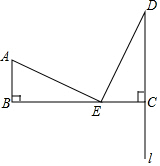 如图,AB=3,BC=8,AB⊥BC,l⊥BC于点C,点E从B向C运动,过点E作ED⊥AE,交l于D.
如图,AB=3,BC=8,AB⊥BC,l⊥BC于点C,点E从B向C运动,过点E作ED⊥AE,交l于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+2017=0 | B. | (x+2017)2=0 | C. | (x+1)2=-2017 | D. | (x+2017)(x-2017)=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com