Question

已知，如图，△AOB的OA、OB两边上的两点M、N.

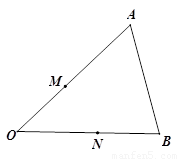
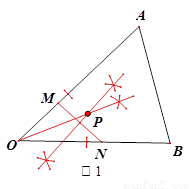
①.求作：点P，使点P到OA、OB的距离相等，且PM＝PN.（尺规作图，不写作法，保留作图痕迹）

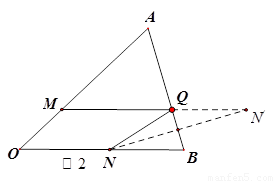
②.在AB上找一点Q使四边形ONQM周长最小。（不一定尺规作图, 可以用三角尺，不写作法）.

 

Answer 1

【答案】

 

【解析】

试题分析：(1)由角平分线的性质可知，求作点P一定在∠AOB的平分线上，由垂直平分线的性质可知，求作点P一定在MN的垂直平分线上，所以点P应是∠AOB的平分线与MN的垂直平分线的交点。

（2）在四边形ONQM周长中，OM、ON的长度已经确定，要使四边形ONQM周长最小，只要保证MQ、NQ的长度之和最小即可。根据最短路径问题的作图知识，先确定任意一点M（或N）关于线段AB的对称点M^/（或N^/），然后连接该对称点与另一点的线段与AB相交的点即为所求点.

试题解析：

解：（1）如图1，点P即为所求点.

（2）如图2，点Q即为所求点.

考点：1、角平分线的作图.2、垂直平分线的作图.