
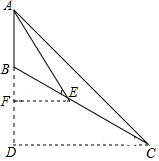
 如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚C处,测得塔顶A的仰角为45°,测量人员沿着坡度i=1:$\sqrt{3}$的山坡BC向上行走100米到达E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈4/3,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)( )
如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚C处,测得塔顶A的仰角为45°,测量人员沿着坡度i=1:$\sqrt{3}$的山坡BC向上行走100米到达E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈4/3,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)( )| A. | 100.5米 | B. | 110.5米 | C. | 113.5米 | D. | 116.5米 |
分析 作EF⊥AD、作EG⊥CD,知EF=DG、FD=EG,由i=$\frac{EG}{CG}$=$\frac{\sqrt{3}}{3}$得FD=EG=50、GC=50$\sqrt{3}$,设BF=x,知DG=EF=$\frac{BF}{tan∠BEF}$=$\sqrt{3}$x、AF=EFtan∠AEF=$\frac{3\sqrt{3}}{4}$x,根据AD=CD列出关于x的方程,解之求得x的值,由BD=BF+DF可得答案.
解答 解:如图,作EF⊥AD于F,作EG⊥CD于G,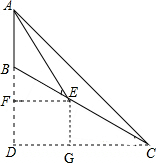
则EF=DG、FD=EG,
∵i=$\frac{EG}{CG}$=$\frac{\sqrt{3}}{3}$,
∴∠ECG=30°,
∵CE=100,
∴FD=EG=ECsin30°=50,GC=ECcos30°=50$\sqrt{3}$,
设BF=x,
∵∠BEF=∠BCD=30°,
∴DG=EF=$\frac{BF}{tan∠BEF}$=$\sqrt{3}$x,
由∠AEF=53°知AF=EFtan∠AEF=$\frac{3\sqrt{3}}{4}$x,
∵∠ACD=45°,
∴AD=CD,即50+$\frac{3\sqrt{3}}{4}$x=$\sqrt{3}$x+50$\sqrt{3}$,
解得:x=150-50$\sqrt{3}$,
则BD=BF+DF=150-50$\sqrt{3}$+50=200-50$\sqrt{3}$≈113.5,
故选:C.
点评 本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度.


科目:初中数学 来源: 题型:选择题
| A. | 3,4,5 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 6,8,10 | D. | 5,12,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
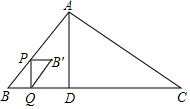 如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
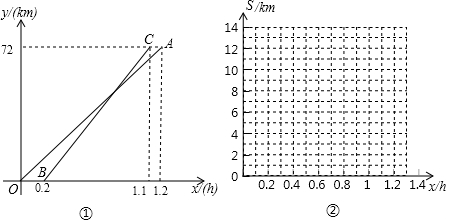
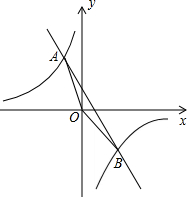 如图,反比例函数y=$\frac{k-1}{x}$(k<0)与一次函数y=kx+b相交于A、B两点,若点A的坐标为(-1,7).
如图,反比例函数y=$\frac{k-1}{x}$(k<0)与一次函数y=kx+b相交于A、B两点,若点A的坐标为(-1,7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
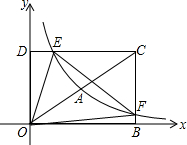 如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com