
 如图,半圆O的直径AC=2$\sqrt{2}$,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为2$\sqrt{2}$-2或$\sqrt{5}$-1.
如图,半圆O的直径AC=2$\sqrt{2}$,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为2$\sqrt{2}$-2或$\sqrt{5}$-1. 分析 分两种情形讨论:①当∠DFE=∠BCE时,可以证明DB=DC,BC=CF,∠DFC=∠DBC=90°即可解决问题.②当∠FDE=∠BCE时,可以证明DF∥BC、△BDF∽△CBD得到$\frac{BD}{CB}=\frac{DF}{BD}$列出方程解决问题.
解答 解: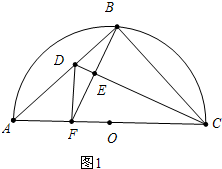 ①如图1,当∠DFE=∠BCE时,
①如图1,当∠DFE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△BEC,
∵AC是直径,
∴∠ABC=90°,
∵BF⊥CD,
∴∠CEB=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠DFE,
∴DB=DF,
∵DE⊥BF,
∴EB=EF,
∴BC=CF,
∵点B为半圆的中点,
∴AB=BC,
∴∠A=45°,
∵∠DBF=∠DFB,∠CBF=∠CFB,∠DBF+∠CBF=90°,
∴∠DFB+∠CFB=90°,
∴∠DFC=∠DFA=90°,
∴∠A=∠ADF=45°,
∴AF=DF=BD,
在RT$△ABC\\;中$中,∵AC=2$\sqrt{2}$,
∴AB=BC=$\frac{\sqrt{2}}{2}$AC=2,
∴FC=2,
∴BD=AF=AC-FC=2$\sqrt{2}$-2,
②如图2,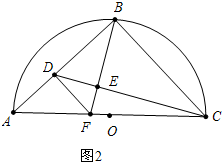 当∠FDE=∠BCE时,
当∠FDE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△CEB,DF∥BC,
∴∠ADF=∠ABC=90°,
∵∠ABC=∠BEC=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠FDE,
∵∠BDF=∠DBC=90°,∠DBF=∠BCD,
∴△BDF∽△CBD,
∴$\frac{BD}{CB}=\frac{DF}{BD}$,
∵∠A=45°,∠ADF=90°,
∴∠AFD=∠A=45°,
∴AD=DF,
设BD=x,由(1)可知:AB=BC=2,AD=DF=2-x,
∴$\frac{x}{2}=\frac{2-x}{x}$,整理得:x2+2x-4=0,
解得:x=-1+$\sqrt{5}$(或-1-$\sqrt{5}$舍弃)
∴BD=$\sqrt{5}$-1.
故答案为2$\sqrt{2}$-2或$\sqrt{5}$-1.
点评 本题考查圆的有关性质、相似三角形的判定和性质、勾股定理等知识,学会分类讨论是解决问题的关键,在解题中用方程的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向右B运动,到点B时停止运动,同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同,设点E的运动路程为x,△AEF的面积为y,求y与x的函数关系的函数关系式y=$\left\{\begin{array}{l}{2x(0≤x≤2)}\\{-12x2+3x(2<x≤4)}\end{array}\right.$,理由:三角形的面积公式.
如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向右B运动,到点B时停止运动,同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同,设点E的运动路程为x,△AEF的面积为y,求y与x的函数关系的函数关系式y=$\left\{\begin{array}{l}{2x(0≤x≤2)}\\{-12x2+3x(2<x≤4)}\end{array}\right.$,理由:三角形的面积公式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩(环) | 7 | 8 | 9 | 10 |
| 甲 | 3次 | 8次 | 5次 | 4次 |
| 乙 | 4次 | 6次 | 6次 | 4次 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由5x=3x-2变形得5x-3x=2 | |
| B. | 由$\frac{2x-1}{3}$=1+$\frac{x-3}{2}$变形得2(2x-1)=1+3(x-3) | |
| C. | 由2(2x-1)-3(x-3)=1变形得4x-2-3x-9=1 | |
| D. | 由2(x+1)=x+7变形得x=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx+2与直线y=$\frac{1}{3}$x相交于点A(3,1),与x轴交于点B.
如图,直线y=kx+2与直线y=$\frac{1}{3}$x相交于点A(3,1),与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 通常温度降到0℃以下,纯净的水会结冰 | |
| B. | 随意翻到一本书的某页,这页的页码是奇数 | |
| C. | 明天的太阳从东方升起 | |
| D. | 在一个不透明的袋子里装有完全相同的6个红色小球,随机抽取一个白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com