
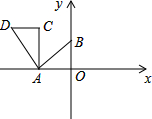
 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )| A. | (4,3) | B. | (-3,4) | C. | (-7,4) | D. | (-7,3) |
分析 先利用坐标轴上点的坐标特征求出A、B两点的坐标,再利用旋转的性质得到AC=OA=4,CD=OB=3,∠OAC=90°,∠ACD=∠AOB=90°,则可判断AC⊥x轴,CD∥x轴,然后根据第二象限点的坐标特征写出D点坐标.
解答 解:当y=0时,$\frac{3}{4}$x+3=0,解得x=-4,则A(-4,0),所以OA=4,
当x=0时,y=$\frac{3}{4}$x+3=3,则B(0,3),所以OB=3,
因为△AOB绕点A逆时针旋转90°后得到△ACD,
所以AC=OA=4,CD=OB=3,∠OAC=90°,∠ACD=∠AOB=90°,
即AC⊥x轴,CD∥x轴,
所以点D的坐标为(-7,4).
故选C.
点评 本题考查了坐标与图形变换-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是确定A点和B点坐标.


科目:初中数学 来源: 题型:解答题
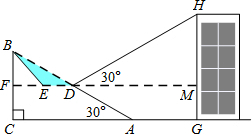 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
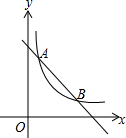 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
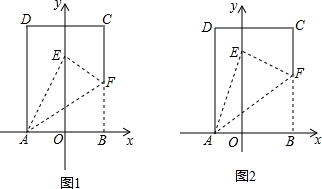 将一个矩形纸片ABCD放置到平面直角坐标系中,点A、B恰落在x轴的正、负半轴上,若将该纸片沿AF折叠,点B恰好落在y轴上的点E处,设OA=1.
将一个矩形纸片ABCD放置到平面直角坐标系中,点A、B恰落在x轴的正、负半轴上,若将该纸片沿AF折叠,点B恰好落在y轴上的点E处,设OA=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
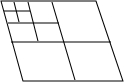 如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )| A. | 2n个 | B. | (2n+1)个 | C. | 3n个 | D. | (3n+1)个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
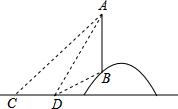 如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°.
如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a10-a7=a3 | B. | (-2a2b)2=-2a4b2 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | (a+b)9÷(a+b)3=(a+b)6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com