
【题目】已知二次函数![]() (
(![]() 为常数).
为常数).
(1)求证:不论![]() 为何值,该函数的图像与
为何值,该函数的图像与![]() 轴总有公共点;
轴总有公共点;
(2)当![]() 取什么值时,该函数的图像与
取什么值时,该函数的图像与![]() 轴的交点在
轴的交点在![]() 轴的下方?
轴的下方?
【答案】(1)见解析;(2)当![]() 时,
时,![]() ,即该函数的图像与
,即该函数的图像与![]() 轴交点的纵坐标是
轴交点的纵坐标是![]() ;(3)当
;(3)当![]() ,即
,即![]() 时,该函数的图像与
时,该函数的图像与![]() 轴的交点在
轴的交点在![]() 轴的下方
轴的下方
【解析】
(1)方法一令![]() ,求解方程的根即可,方法二根据根的判别式判断,(2)根据
,求解方程的根即可,方法二根据根的判别式判断,(2)根据![]() 轴的下方的点的纵坐标为负,列不等式即可解题.
轴的下方的点的纵坐标为负,列不等式即可解题.
(1)证明:
方法一:当![]() 时,
时,![]() .
.
解得![]() ,
,![]() .
.
当![]() ,即
,即![]() 时,方程有两个相等的实数根;当
时,方程有两个相等的实数根;当![]() ,即
,即![]() 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.
所以,不论![]() 为何值,该函数的图像与
为何值,该函数的图像与![]() 轴总有公共点.
轴总有公共点.
方法二:将原表达式化为![]() .
.
因为一元二次方程![]() 的根的判别式
的根的判别式![]() .
.
所以,不论![]() 为何值,该函数的图像与
为何值,该函数的图像与![]() 轴总有公共点.
轴总有公共点.
(2)解:当![]() 时,
时,![]() ,即该函数的图像与
,即该函数的图像与![]() 轴交点的纵坐标是
轴交点的纵坐标是![]() .
.
∴当![]() ,即
,即![]() 时,该函数的图像与
时,该函数的图像与![]() 轴的交点在
轴的交点在![]() 轴的下方.
轴的下方.


科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要30名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生18人,女生12人.
(1)若从这30人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,且OA、OB分别与反比例函数y=![]() (x>0)、y=﹣
(x>0)、y=﹣![]() (x<0)的图象交于A、B两点,则tan∠OAB的值是( )
(x<0)的图象交于A、B两点,则tan∠OAB的值是( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
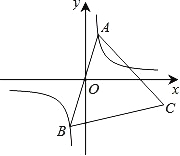
【题目】如图,已知点A是双曲线![]() 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数![]() 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出![]() 时x的取值范围.
时x的取值范围.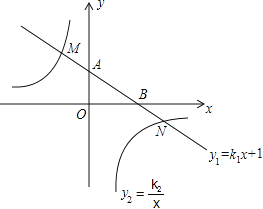
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB = AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
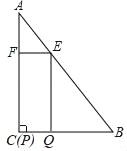
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com