练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    问题：探索等腰三角形—腰上的高与底边所成的角与顶角的关系．

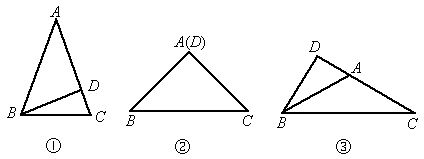
    (1)为了解决这个问题，我们可从特殊情形入手，如图①，在△ABC中，AB=AC，∠A=40°，BD是边AC上的高，则∠DBC=________°．如图②，在△ABC中，AB=AC，∠A=90°，BD是边AC上的高，则∠DBC=________°．如图③，在△ABC中，AB=AC，∠A=120°，BD是边AC上的高，则∠DBC=________°；

    (2)猜想，∠A与∠DBC的关系是________；

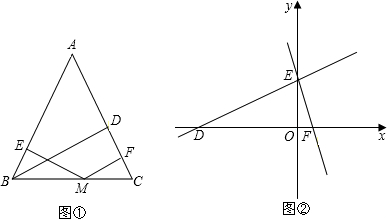
    (3)对上述猜想，你能作出解释吗?(提示：作AE⊥BC，垂足为E)

    答案：略
    解析：

    (1)20，45，60；(2)∠A=2∠DBC；(3)略


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法．请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高．
    （1）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1，h2．
    A、若M在线段BC上，请你结合图形①证明：h1+h2=h；
    B、当点M在BC的延长线上时，h1，h2，h之间的关系为
     
    ．（请直接写出结论，不必证明）
    （2）如图②，在平面直角坐标系中有两条直线l1：y=
    34
    x+6；l2：y=-3x+6．若l2上的一点M到l1的距离是3，请你利用以上结论求解点M的坐标．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    探究学习：探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法．请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高（如图1）．
    （1）若等腰△ABC的面积为24 cm2，腰的长为8 cm，则腰AC上的高BD的长为
     
    cm；
    （2）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1、h2．
    ①若M在线段BC上，请你结合图2证明：h1+h2=h；
    ②当点M在BC延长线上时，h1、h2、h之间的关系为
     
    ．（直接写出结论，不必证明）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2011年江苏省盐城市阜宁县GSJY中考数学模拟试卷（解析版） 题型：解答题

    探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法．请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高．
    （1）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1，h2．
    A、若M在线段BC上，请你结合图形①证明：h1+h2=h；
    B、当点M在BC的延长线上时，h1，h2，h之间的关系为______．（请直接写出结论，不必证明）
    （2）如图②，在平面直角坐标系中有两条直线l1：y=x+6；l2：y=-3x+6．若l2上的一点M到l1的距离是3，请你利用以上结论求解点M的坐标．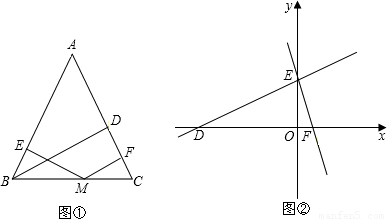

    查看答案和解析>>

    科目：初中数学 来源：2011年浙江省杭州市中考数学模拟试卷（19）（解析版） 题型：解答题

    探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法．请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高．
    （1）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1，h2．
    A、若M在线段BC上，请你结合图形①证明：h1+h2=h；
    B、当点M在BC的延长线上时，h1，h2，h之间的关系为______．（请直接写出结论，不必证明）
    （2）如图②，在平面直角坐标系中有两条直线l1：y=x+6；l2：y=-3x+6．若l2上的一点M到l1的距离是3，请你利用以上结论求解点M的坐标．

    查看答案和解析>>

    同步练习册答案