
分析 (1)根据有理数的乘法和加法可以解答本题;
(2)根据有理数的加减法和乘除法可以解答本题;
(3)根据乘法分配律可以解答本题.
解答 解:(1)($\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$)×(-4)×6
=($\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$)×(-24)
=-12-16+6
=-22;
(2)-12-[$\frac{2}{3}$+(-12)÷6]2×(-$\frac{3}{4}$)2
=-1-[$\frac{2}{3}-2$]×$\frac{9}{16}$
=-1+$\frac{4}{3}×\frac{9}{16}$
=-1+$\frac{3}{4}$
=-$\frac{1}{4}$;
(3)9×$\frac{3}{4}$-(-9)×$\frac{1}{2}$+9×(-$\frac{1}{4}$)
=9×$\frac{3}{4}$+9×$\frac{1}{2}$+9×(-$\frac{1}{4}$)
=9×($\frac{3}{4}+\frac{1}{2}-\frac{1}{4}$)
=9×1
=9.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
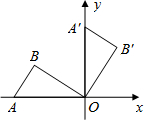 如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.
如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 组别 | A型 | B型 | AB型 | O型 |
| 频数 | b | c | d | 6 |
| 频率 | a | 0.35 | 0.1 | e |
| A. | 16人 | B. | 14人 | C. | 4人 | D. | 6人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com