
分析 先根据一元二次方程的解的定义得a2+a-2016=0,即a2=-a+2016,则原式化为a2+2a+b=-a+2016+2a+b=2016+a+b,然后利用根与系数的关系求解.
解答 :∵a是方程x2+x-2016=0的实数根,
∴a2+a-2016=0,即a2=-a+2016,
∴a2+2a+b=-a+2016+2a+b
=2016+a+b,
∵a,b是方程x2+x-2016=0的两个不相等的实数根,
∴a+b=-1,
∴a2+2a+b=2016-1=2015.
故答案为2015.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的解.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:填空题
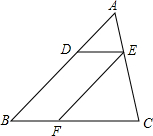 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
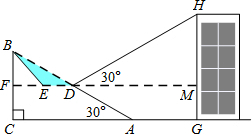 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
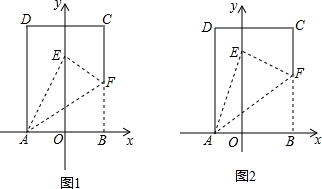 将一个矩形纸片ABCD放置到平面直角坐标系中,点A、B恰落在x轴的正、负半轴上,若将该纸片沿AF折叠,点B恰好落在y轴上的点E处,设OA=1.
将一个矩形纸片ABCD放置到平面直角坐标系中,点A、B恰落在x轴的正、负半轴上,若将该纸片沿AF折叠,点B恰好落在y轴上的点E处,设OA=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com