
某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品,根据市场调研,发现如下两种信息:
信息一:销售甲款护肤品所获利润y(元)与销售量x(件)之间存在二次函数关系y=ax2+bx.在x=10时,y=140;当x=30时,y=360.
信息二:销售乙款护肤品所获利润y(元)与销售量x(件)之间存在正比例函数关系y=3x.请根据以上信息,解答下列问题;
(1)求信息一中二次函数的表达式;
(2)该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件,请设计一个营销方案,使销售甲、乙两款护肤品获得的利润之和最大,并求出最大利润.
(1)y=-0.1x2+15x;(2)购进甲产品60件,购进一产品40件,最大利润是660元.
解析试题分析:(1)把两组数据代入二次函数解析式,然后利用待定系数法求解即可;
(2)设购进甲产品m件,购进乙产品(10-m)件,销售甲、乙两种产品获得的利润之和为W元,根据总利润等于两种产品的利润的和列式整理得到W与m的函数关系式,再根据二次函数的最值问题解答.
试题解析:(1)∵当x=10时,y=140;当x=30时,y=360,
∴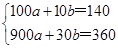 ,解得:a=?0.1,b=15,
,解得:a=?0.1,b=15,
所以,二次函数解析式为y=-0.1x2+15x;
(2)设购进甲产品m件,购进乙产品(100-m)件,销售甲、乙两种产品获得的利润之和为W元,
则W=-0.1m2+15m+3(100-m)=-0.1m2+12m+300=-0.1(m-60)2+660,
∵-0.1<0,
∴当m=60时,W有最大值660元,
∴购进甲产品60件,购进一产品40件,销售甲、乙两种产品获得的利润之和最大,最大利润是660元.
考点:二次函数的应用.


科目:初中数学 来源: 题型:解答题
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足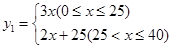 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.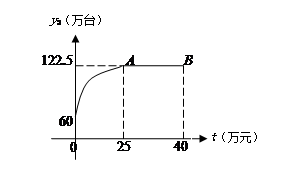
(1)结合图象,写出y2(万台)与外地广告费用t(万元)之间的函数关系式;
(2)求该产品的销售总量y(万台)与外地广告费用t(万元)之间的函数关系式;
(3)如何安排广告费用才能使销售总量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).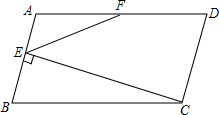
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
近期,海峡两岸关系的气氛大为改善.大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售.某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
| 每千克售价(元) | 40 | 39 | 38 | 37 | … | 30 |
| 每天销量(千克) | 60 | 65 | 70 | 75 | … | 110 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某区政府大力扶持大学生创业.李刚在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500.
(1)设李刚每月获得利润为w(元),当销售单价定为每台多少元时,每月可获得最大利润?
(2)如果李刚想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李刚想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.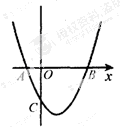
(1)点A的坐标为 点B的坐标为 ,点C的坐标为 ;
(2)设抛物线y=x2-2x-3的顶点坐标为M,求四边形ABMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)已知二次函数 ,请你化成
,请你化成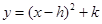 的形式,并在直角坐标系中画出
的形式,并在直角坐标系中画出 的图象;
的图象;
(2)如果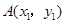 ,
,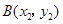 是(1)中图象上的两点,且
是(1)中图象上的两点,且 ,请直接写出
,请直接写出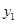 、
、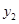 的大小关系;
的大小关系;
(3)利用(1)中的图象表示出方程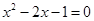 的根来,要求保留画图痕迹,说明结果.
的根来,要求保留画图痕迹,说明结果.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.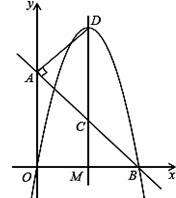
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com