
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
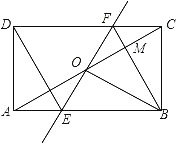
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】试题分析:①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;
③先证△BEF是等边三角形得出BF=EF,再证DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.
①∵矩形ABCD中,O为AC中点, ∴OB=OC, ∵∠COB=60°, ∴△OBC是等边三角形, ∴OB=BC,
∵FO=FC, ∴FB垂直平分OC, 故①正确;
②∵FB垂直平分OC, ∴△CMB≌△OMB, ∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO, ∴△FOC≌△EOA,
∴FO=EO, 易得OB⊥EF, ∴△OMB≌△OEB, ∴△EOB≌△CMB, 故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE, ∴△BEF是等边三角形, ∴BF=EF,
∵DF∥BE且DF=BE, ∴四边形DEBF是平行四边形, ∴DE=BF, ∴DE=EF, 故③正确;
④在直角△BOE中∵∠3=30°, ∴BE=2OE, ∵∠OAE=∠AOE=30°, ∴AE=OE, ∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2, 故④错误;
所以其中正确结论的个数为3个


科目:初中数学 来源: 题型:
【题目】某人设计了一个游戏,在网吧征求了三位游戏迷的意见,就宣传“本游戏深受大家欢迎”,这种做法是错误的,原因是( )
A. 没有经过专家鉴定
B. 应调查4位游戏迷
C. 调查数量太少,且不具有代表性
D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们知道因式分解与整式乘法是互逆关系,那么逆用乘法公式(x+a)(x+b)=x2+(a+b)x+ab,即x2+(a+b)x+ab=(x+a)(x+b),是否可以因式分解呢?当然可以,而且也很简单.如:x2+4x+3=x2+(1+3)x+1×3=(x+1)(x+3);
请你仿照上述方法分解因式:x2-7x-18;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com