
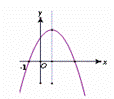
已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图像如图所示,
有下列结论:①abc>0,②b2-4ac<0,③a-b+c>0,④4a-2b+c<0,
其中正确结论的个数是( )

A.1 B.2 C.3 D.4
A
【![]() 解析】首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,根据抛物线与x轴是否有交点确定b2-4ac的取值范围,根据图象和x=2的函数值即可确定4a+2b+c的取值范围,根据x=1的函数值可以确定b<a+c是否成立.
解析】首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,根据抛物线与x轴是否有交点确定b2-4ac的取值范围,根据图象和x=2的函数值即可确定4a+2b+c的取值范围,根据x=1的函数值可以确定b<a+c是否成立.
解答:解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=-![]() ,
,
∴b>0,
∵抛物线与y轴的交![]() 点在x轴的上方,
点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道抛物线与x轴有两个交点,![]()
∴b2-4ac>0,故②错误;
根据图象知道当x=-1时,y=a-b+c=0,
故③错误;
∵抛物线开口向下,x=-1时抛物线与Y轴相交,
∴x<1时的抛物线位于x轴下方,即y<0,
∴当x=-2时,y=a(-2)2+(-2)b+c=![]() 4a-2b+c<0
4a-2b+c<0![]() ,
,
故④正确.
故选A.
点评:此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与![]() 方程之间的转换,根的判别式的熟练运用.
方程之间的转换,根的判别式的熟练运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:选择题
已知二次函数y=ax²+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax²+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax²+bx+c(c≠0)的图像如图4所示,下列说法错误的是:
(A)图像关于直线x=1对称
(B)函数y=ax²+bx+c(c ≠0)的最小值是 -4
(C)-1和3是方程ax²+bx+c=0(c ≠0)的两个根
(D)当x<1时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com