

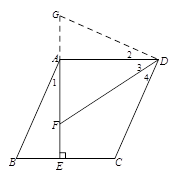
 (2)解:(1)中的结论仍然成立.
(2)解:(1)中的结论仍然成立. 或
或 或
或


科目:初中数学 来源:不详 题型:解答题

 沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到
沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到 (如图②).小明认为
(如图②).小明认为 是等腰三角形,你同意吗?请说明理由.
是等腰三角形,你同意吗?请说明理由.
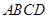 沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点
沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点 处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中
处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中 的大小.
的大小.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
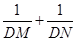 是否为定值.若是.请求出该定值;若不是.请说明理由。
是否为定值.若是.请求出该定值;若不是.请说明理由。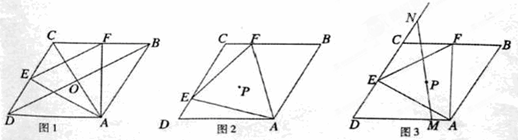
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD; ∠BAD, (1)中的结论是否仍然成立?不用证明.
∠BAD, (1)中的结论是否仍然成立?不用证明.  ∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
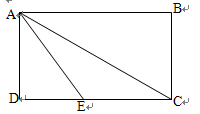
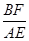 的值。
的值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com