
【题目】如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y= ![]() 的图象的一个交点为A(1,m).过点B作AB的垂线BD,与反比例函数y=
的图象的一个交点为A(1,m).过点B作AB的垂线BD,与反比例函数y= ![]() (x>0)的图象交于点D(n,﹣2).
(x>0)的图象交于点D(n,﹣2).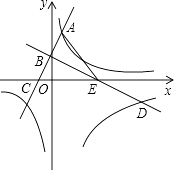
(1)求k1和k2的值;
(2)若直线AB、BD分别交x轴于点C、E,试问在y轴上是否存在一个点F,使得△BDF∽△ACE?若存在,求出点F的坐标;若不存在,请说明理由.
【答案】
(1)
解:将A(1,m)代入一次函数y=2x+2中,得:m=2+2=4,即A(1,4),
将A(1,4)代入反比例解析式y= ![]() 得:k1=4;
得:k1=4;
过A作AM⊥y轴,过D作DN⊥y轴,
∴∠AMB=∠DNB=90°,
∴∠BAM+∠ABM=90°,
∵AC⊥BD,即∠ABD=90°,
∴∠ABM+∠DBN=90°,
∴∠BAM=∠DBN,
∴△ABM∽△BDN,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DN=8,
∴D(8,﹣2),
将D坐标代入y= ![]() 得:k2=﹣16
得:k2=﹣16
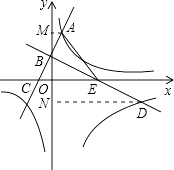
(2)
解:符合条件的F坐标为(0,﹣8),理由为:
由y=2x+2,求出C坐标为(﹣1,0),
∵OB=ON=2,DN=8,
∴OE=4,
可得AE=5,CE=5,AC=2 ![]() ,BD=4
,BD=4 ![]() ,∠EBO=∠ACE=∠EAC,
,∠EBO=∠ACE=∠EAC,
若△BDF∽△ACE,则 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:BF=10,
则F(0,﹣8).
综上所述:F点坐标为(0,﹣8)时,△BDF∽△ACE.
【解析】(1)将A坐标代入一次函数解析式中求出m的值,确定出A的坐标,将A坐标代入反比例函数y= ![]() 中即可求出k1的值;过A作AM垂直于y轴,过D作DN垂直于y轴,可得出一对直角相等,再由AC垂直于BD,利用同角的余角相等得到一对角相等,利用两对对应角相等的两三角形相似得到三角形ABM与三角形BDN相似,由相似得比例,求出DN的长,确定出D的坐标,代入反比例函数y=
中即可求出k1的值;过A作AM垂直于y轴,过D作DN垂直于y轴,可得出一对直角相等,再由AC垂直于BD,利用同角的余角相等得到一对角相等,利用两对对应角相等的两三角形相似得到三角形ABM与三角形BDN相似,由相似得比例,求出DN的长,确定出D的坐标,代入反比例函数y= ![]() 中即可求出k2的值;(2)在y轴上存在一个点F,使得△BDF∽△ACE,此时F(0,﹣8),理由为:由y=2x+2求出C坐标,由OB=ON=2,DN=8,可得出OE为三角形BDN的中位线,求出OE的长,进而利用两点间的距离公式求出AE,CE,AC,BD的长,以及∠EBO=∠ACE=∠EAC,若△BDF∽△ACE,得到比例式,求出BF的长,即可确定出此时F的坐标,
中即可求出k2的值;(2)在y轴上存在一个点F,使得△BDF∽△ACE,此时F(0,﹣8),理由为:由y=2x+2求出C坐标,由OB=ON=2,DN=8,可得出OE为三角形BDN的中位线,求出OE的长,进而利用两点间的距离公式求出AE,CE,AC,BD的长,以及∠EBO=∠ACE=∠EAC,若△BDF∽△ACE,得到比例式,求出BF的长,即可确定出此时F的坐标,
再利用BD=DF时,进而得出即可.
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小),还要掌握反比例函数的图象(反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α. 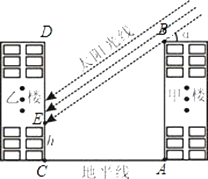
(1)用含α的式子表示h(不必指出α的取值范围);
(2)当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 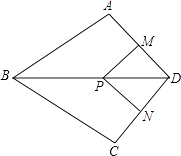
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( ) 
A.1
B.![]()
C.4﹣2 ![]()
D.3 ![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.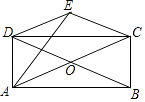
(1)求证:四边形OCED是菱形;
(2)连接AE,若AB=6cm,BC= ![]() cm.
cm.
①求sin∠EAD的值;
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC. 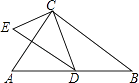
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2017年中考,某中学对全校九年级学生进行了一次数学期末模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题: 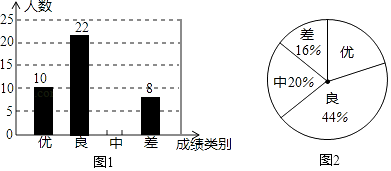
(1)在这次调查中,样本中表示成绩类别为“中”的人数;
(2)将条形统计图补充完整;
(3)若该中学九年级共有800人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com