
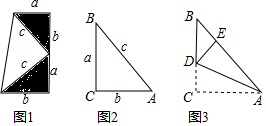
分析 (1)根据方法一和二所列的梯形的面积相等列式可得a、b、c之间的等量关系;
(2)先由勾股定理得:a2+b2=c2=25①,将a-b=1两边同时平方得:a2-2ab+b2=1②,两式可得:ab=12,可以求三角形ABC的面积,由a+b=$\sqrt{(a+b)^{2}}$可得a+b的值,可以计算三角形ABC的周长;
(3)由折叠得:DC=DE,∠DEA=∠C=90°,AE=AC=6,设BD=x,在Rt△BDE中,由勾股定理列方程可得结论.
解答 解:(1)∵S梯形=$\frac{1}{2}$(a+b)•(a+b),S梯形=2×$\frac{1}{2}$ab+$\frac{1}{2}$c2,
∴$\frac{1}{2}$(a+b)•(a+b)=2×$\frac{1}{2}$ab+$\frac{1}{2}$c2,
(a+b)2=2ab+c2,
∴a2+b2=c2;
(2)如图2,由勾股定理得:a2+b2=c2=25①,
∵a-b=1,
∴a2-2ab+b2=1②,
把①代入②得:25-2ab=1,
ab=12,
∴S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$×12=6,
∵a+b=$\sqrt{(a+b)^{2}}$=$\sqrt{{a}^{2}+2ab+{b}^{2}}$=$\sqrt{25+2×12}$=7,
∴△ABC的周长=7+5=12;
(3)如图3,由折叠得:DC=DE,∠DEA=∠C=90°,AE=AC=6,
设BD=x,则CD=DE=8-x,
在Rt△ABC中,由勾股定理得:AB=10,
在Rt△BDE中,由勾股定理得:x2=42+(8-x)2,
x=5,
∴BD=5.
点评 本题考查了完全平方公式、勾股定理的证明和运用、三角形面积、折叠的性质,熟练掌握利用面积法证明勾股定理,本题难度适中.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
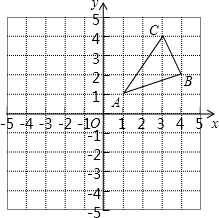 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×10-4 | B. | 3×10-5 | C. | 3×10-6 | D. | 0.3×10-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 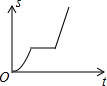 | B. | 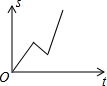 | C. | 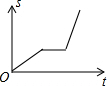 | D. | 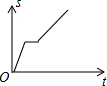 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com