
ЁОЬтФПЁПФГАрЪІЩњзщжЏжВЪїЛюЖЏЃЌЩЯЮч8ЪБДгбЇаЃГіЗЂЃЌЕНжВЪїЕиЕуКѓдТЗЗЕаЃЃЌШчЭМЮЊЪІЩњРыаЃТЗГЬsгыЪБМфtжЎМфЕФЭМЯѓЃЌЧыЛиД№ЯТСаЮЪЬтЃК
![]() ЪдаДГіЪІЩњЗЕаЃЪБЕФsгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЪІЩњКЮЪБЛиЕНбЇаЃЃЛ
ЪдаДГіЪІЩњЗЕаЃЪБЕФsгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЪІЩњКЮЪБЛиЕНбЇаЃЃЛ
![]() ШчЙћЪІЩњЦяздааГЕЩЯЮч8ЪБГіЗЂЃЌЕНжВЪїЕиЕуКѓЃЌжВЪїаш2аЁЪБЃЌвЊЧѓ14ЪБЧАЗЕЛиЕНбЇаЃЃЌЭљЗЕЦНОљЫйЖШЗжБ№ЮЊУПЪБ10kmЁЂ8kmЃЌЯжгаAЁЂBЁЂCЁЂDЫФИіжВЪїЕугыбЇаЃЕФТЗГЬЗжБ№ЪЧ13kmЁЂ15kmЁЂ17kmЁЂ19kmЃЌЪдЭЈЙ§МЦЫуЫЕУїФФМИИіжВЪїЕуЗћКЯвЊЧѓЃЎ
ШчЙћЪІЩњЦяздааГЕЩЯЮч8ЪБГіЗЂЃЌЕНжВЪїЕиЕуКѓЃЌжВЪїаш2аЁЪБЃЌвЊЧѓ14ЪБЧАЗЕЛиЕНбЇаЃЃЌЭљЗЕЦНОљЫйЖШЗжБ№ЮЊУПЪБ10kmЁЂ8kmЃЌЯжгаAЁЂBЁЂCЁЂDЫФИіжВЪїЕугыбЇаЃЕФТЗГЬЗжБ№ЪЧ13kmЁЂ15kmЁЂ17kmЁЂ19kmЃЌЪдЭЈЙ§МЦЫуЫЕУїФФМИИіжВЪїЕуЗћКЯвЊЧѓЃЎ

ЁОД№АИЁПЃЈ1ЃЉЪІЩњдк13ЪБ36ЗжЛиЕНбЇаЃЃЛ(2)МћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШИљОнЪІЩњЗЕаЃЪБЕФТЗГЬгыЪБМфжЎМфЕФЙиЯЕСаГіКЏЪ§НтЮіЪНЃЌШЛКѓПДЭМНЋСНзщЖдгІsгыtЕФжЕДњШыПЩЕУЕНвЛИіЖўдЊвЛДЮЗНГЬзщЃЌНтДЫЗНГЬзщПЩЕУКЏЪ§НтЮіЪНЃЎЕБЗЕЛибЇаЃЪБОЭЪЧsЮЊ0ЪБЃЌtЕФжЕЃЛ
ЃЈ2ЃЉЯШЩшЗћКЯбЇаЃвЊЧѓЕФжВЪїЕугыбЇаЃЕФТЗГЬЮЊxЃЈkmЃЉЃЌШЛКѓИљОнЭљЗЕЕФЦНОљЫйЖШЁЂТЗГЬКЭЪБМфЕУЕНвЛИіВЛЕШЪНЃЌНтДЫВЛЕШЪНПЩЕУЕНxЕФШЁжЕЗЖЮЇЃЌдйШЗЖЈжВЪїЕуЪЧЗёЗћКЯвЊЧѓЃЎ
ЪдЬтНтЮіЃК ![]() ЩшЪІЩњЗЕаЃЪБЕФКЏЪ§НтЮіЪНЮЊ
ЩшЪІЩњЗЕаЃЪБЕФКЏЪ§НтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ШчЭМЫљЪОЃЌАб![]() ЁЂ
ЁЂ![]() ДњШыЩЯЪНжаЕУЃК
ДњШыЩЯЪНжаЕУЃК
![]() ЃЌ
ЃЌ
НтДЫЗНГЬзщЕУЃЌ ![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ
![]() ЪБ36Зж
ЪБ36Зж
дђЪІЩњдк13ЪБ36ЗжЛиЕНбЇаЃЃЛ
![]() ЩшЗћКЯбЇаЃвЊЧѓЕФжВЪїЕугыбЇаЃЕФТЗГЬЮЊ
ЩшЗћКЯбЇаЃвЊЧѓЕФжВЪїЕугыбЇаЃЕФТЗГЬЮЊ![]() ЃЌ
ЃЌ
гЩЬтвтЕУЃК ![]() ЃЌ
ЃЌ
НтЕУЃК ![]() ЃЌ
ЃЌ
![]() ЁЂBЁЂCЁЂDЫФИіжВЪїЕугыбЇаЃЕФТЗГЬЗжБ№ЪЧ13kmЁЂ15kmЁЂ17kmЁЂ19kmЃЌ
ЁЂBЁЂCЁЂDЫФИіжВЪїЕугыбЇаЃЕФТЗГЬЗжБ№ЪЧ13kmЁЂ15kmЁЂ17kmЁЂ19kmЃЌ
![]() ЃЌ
ЃЌ
Д№ЃК13kmЃЌ15kmЃЌ17kmжВЪїЕуЗћКЯбЇаЃЕФвЊЧѓЃЎ


 ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ
ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ ВНВНИпПкЫуЬтПЈЯЕСаД№АИ
ВНВНИпПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтЭЌбЇЖдЬхг§ЛюЖЏЕФЯВАЎЧщПіЃЌФГаЃЩшМЦСЫЁАФузюЯВЛЖЕФЬхг§ЛюЖЏЪЧФФвЛЯюЃЈНіЯовЛЯюЃЉЁБЕФЕїВщЮЪОэЃЎИУаЃЖдБОаЃбЇЩњНјааЫцЛњГщбљЕїВщЃЌвдЯТЪЧИљОнЕїВщЪ§ОнЕУЕНЕФЭГМЦЭМЕФвЛВПЗжЃЎЧыИљОнвдЩЯаХЯЂНтД№вдЯТЮЪЬтЃК
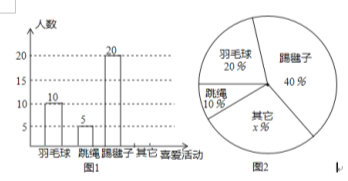
ЃЈ1ЃЉИУаЃЖдЖрЩйУћбЇЩњНјааСЫГщбљЕїВщЃП
ЃЈ2ЃЉЂйЧыВЙШЋЭМ1ВЂБъЩЯЪ§Он ЂкЭМ2жаx= ЃЎ
ЃЈ3ЃЉШєИУаЃЙВгабЇЩњ900ШЫЃЌЧыФуЙРМЦИУаЃзюЯВЛЖЬјЩўЯюФПЕФбЇЩњдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ ABCD жаЃЌЕу G ЪЧБп CD ЩЯвЛЕуЃЈВЛгыЖЫЕу CЃЌD жиКЯЃЉЃЌвд CGЮЊБпдке§ЗНаЮ ABCD Этзїе§ЗНаЮ CEFGЃЌЧв BЁЂCЁЂE Ш§ЕудкЭЌвЛжБЯпЩЯЃЌЩше§ЗНаЮ ABCD КЭе§ЗНаЮ CEFG ЕФБпГЄЗжБ№ЮЊ a КЭ bЃЎ
ЃЈ1ЃЉЗжБ№гУКЌ aЃЌb ЕФДњЪ§ЪНБэЪОЭМ 1 КЭЭМ 2 жавѕгАВПЗжЕФУцЛ§ S1ЁЂS2ЃЛ
ЃЈ2ЃЉШчЙћ a+b=5ЃЌab=3ЃЌЧѓ S1 ЕФжЕЃЛ
ЃЈ3ЃЉЕБ S1ЃМS2 ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШёНЧЁїABCжаЃЌЁЯACB=30ЁуЃЌAB=5ЃЌЁїABCЕФУцЛ§ЮЊ23ЃЎ
ЃЈ1ЃЉШєЕуPдкABБпЩЯЧвCP=![]() ЃЌDЃЌEЗжБ№ЮЊБпACЃЌBCЩЯЕФЖЏЕуЃЎЧѓЁїPDEжмГЄЕФзюаЁжЕЃЛ
ЃЌDЃЌEЗжБ№ЮЊБпACЃЌBCЩЯЕФЖЏЕуЃЎЧѓЁїPDEжмГЄЕФзюаЁжЕЃЛ
ЃЈ2ЃЉМйЩшвЛжЛаЁбђдкЁїABCЧјгђФкЃЌДгТЗБпABФГЕуГіЗЂХмЕНЫЎЙЕБпACКШЫЎЃЌШЛКѓХмЯђТЗБпBCГдВнЃЌдйХмЛиГіЗЂЕуДІанЯЂЃЌжБНгаДГіаЁбђЫљХмЕФзюЖЬТЗГЬЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуPЪЧжБЯп![]() ЩЯвЛЖЈЕуЃЌЕуAЪЧxжсЩЯвЛЖЏЕу
ЩЯвЛЖЈЕуЃЌЕуAЪЧxжсЩЯвЛЖЏЕу![]() ВЛгыдЕужиКЯ
ВЛгыдЕужиКЯ![]() ЃЌСЌНгPAЃЌЙ§ЕуPзї
ЃЌСЌНгPAЃЌЙ§ЕуPзї![]() ЃЌНЛyжсгкЕуBЃЌЬНОПЯпЖЮPAгыPBЕФЪ§СПЙиЯЕЃЎ
ЃЌНЛyжсгкЕуBЃЌЬНОПЯпЖЮPAгыPBЕФЪ§СПЙиЯЕЃЎ

![]() 1
1![]() ШчЭМ
ШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() жсЪБЃЌЙлВьЭМаЮЗЂЯжЯпЖЮPAгыPBЕФЪ§СПЙиЯЕЪЧ______ЃЛ
жсЪБЃЌЙлВьЭМаЮЗЂЯжЯпЖЮPAгыPBЕФЪ§СПЙиЯЕЪЧ______ЃЛ
![]() 2
2![]() ЕБPAгыxжсВЛДЙжБЪБЃЌдкЭМ
ЕБPAгыxжсВЛДЙжБЪБЃЌдкЭМ![]() жаЛГіЭМаЮЃЌЯпЖЮPAгыPBЕФЪ§СПЙиЯЕЪЧЗёгы
жаЛГіЭМаЮЃЌЯпЖЮPAгыPBЕФЪ§СПЙиЯЕЪЧЗёгы![]() Ђё
Ђё![]() ЫљЕУНсЙћЯрЭЌЃПаДГіФуЕФВТЯыВЂМгвджЄУїЃЛ
ЫљЕУНсЙћЯрЭЌЃПаДГіФуЕФВТЯыВЂМгвджЄУїЃЛ
![]() 3
3 ![]() ЮЊКЮжЕЪБЃЌЯпЖЮ
ЮЊКЮжЕЪБЃЌЯпЖЮ![]() ЃПДЫЪБ
ЃПДЫЪБ![]() ЕФЖШЪ§ЪЧЖрЩйЃЌЮЊЪВУДЃП
ЕФЖШЪ§ЪЧЖрЩйЃЌЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЕуEЁЂPдкБпABЩЯЃЌЧвAE=BPЃЌЙ§ЕуEЁЂPзїBCЕФЦНааЯпЃЌЗжБ№НЛACгкЕуFЁЂQЃЌМЧЁїAEFЕФУцЛ§ЮЊS1 ЃЌ ЫФБпаЮEFQPЕФУцЛ§ЮЊS2 ЃЌ ЫФБпаЮPQCBЕФУцЛ§ЮЊS3 ЃЎ 
ЃЈ1ЃЉЧѓжЄЃКEF+PQ=BCЃЛ
ЃЈ2ЃЉШєS1+S3=S2 ЃЌ Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєS3ЉS1=S2 ЃЌ жБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=aЃЈx-2ЃЉ2+cЃЈaЃО0ЃЉЃЌЕБздБфСПxЗжБ№ШЁ ![]() ЁЂ3ЁЂ0ЪБЃЌЖдгІЕФКЏЪ§жЕЗжБ№ЃКy1 ЃЌ y2 ЃЌ y3 ЃЌ дђy1 ЃЌ y2 ЃЌ y3ЕФДѓаЁЙиЯЕе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЁЂ3ЁЂ0ЪБЃЌЖдгІЕФКЏЪ§жЕЗжБ№ЃКy1 ЃЌ y2 ЃЌ y3 ЃЌ дђy1 ЃЌ y2 ЃЌ y3ЕФДѓаЁЙиЯЕе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.y3<y2<y1
B.y1<y2<y3
C.y2<y1<y3
D.y3<y1<y2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
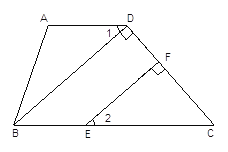
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯA=104ЁуЃЁЯ2ЃЌЁЯABC=76ЁуЃЋЁЯ2ЃЌBDЁЭCDгкDЃЌEFЁЭCDгкFЃЎ
ЧѓжЄЃКЁЯ1=ЁЯ2ЃЎЧыФуЭъГЩЯТУцжЄУїЙ§ГЬЃЎ
жЄУїЃКвђЮЊЁЯAЃН104ЁуЃЁЯ2ЃЌЁЯABCЃН76ЁуЃЋЁЯ2ЃЌЃЈ ЃЉ
Ыљвд ЁЯAЃЋЁЯABCЃН104ЁуЃЁЯ2ЃЋ76ЁуЃЋЁЯ2ЃЌ ЃЈ ЕШЪНаджЪ ЃЉ
МД ЁЯAЃЋЁЯABCЃН180Ёу
Ыљвд ADЁЮBCЃЌЃЈ ЃЉ
Ыљвд ЁЯ1ЃНЁЯDBCЃЌЃЈ ЃЉ
вђЮЊ BDЁЭDCЃЌEFЁЭDCЃЌЃЈ ЃЉ
Ыљвд ЁЯBDC=90Ёу,ЁЯEFC=90Ёу,( )
Ыљвд ЁЯBDC=ЁЯEFC,
Ыљвд BDЁЮ ЃЌЃЈ ЃЉ
Ыљвд ЁЯ2ЃНЁЯDBCЃЌЃЈ ЃЉ
Ыљвд ЁЯ1ЃНЁЯ2 ЃЈ ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНт
Ёп![]() ЃМ
ЃМ![]() ЃМ
ЃМ![]() ЃЌМД2ЃМ
ЃЌМД2ЃМ![]() ЃМ3ЃЎ
ЃМ3ЃЎ
Ёр![]() ЕФећЪ§ВПЗжЮЊ2ЃЌаЁЪ§ВПЗжЮЊ
ЕФећЪ§ВПЗжЮЊ2ЃЌаЁЪ§ВПЗжЮЊ![]() Љ2ЃЌ
Љ2ЃЌ
Ёр1ЃМ![]() Љ1ЃМ2
Љ1ЃМ2
Ёр![]() Љ1ЕФећЪ§ВПЗжЮЊ1ЃЎ
Љ1ЕФећЪ§ВПЗжЮЊ1ЃЎ
Ёр![]() Љ1ЕФаЁЪ§ВПЗжЮЊ
Љ1ЕФаЁЪ§ВПЗжЮЊ![]() Љ2
Љ2
НтОіЮЪЬтЃКвбжЊЃКaЪЧ![]() Љ3ЕФећЪ§ВПЗжЃЌbЪЧ
Љ3ЕФећЪ§ВПЗжЃЌbЪЧ![]() Љ3ЕФаЁЪ§ВПЗжЃЌ
Љ3ЕФаЁЪ§ВПЗжЃЌ
ЧѓЃКЃЈ1ЃЉaЃЌbЕФжЕЃЛ
ЃЈ2ЃЉЃЈЉaЃЉ3+ЃЈb+4ЃЉ2ЕФЦНЗНИљЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com