
【题目】如图,已知△ABC和△DCE是等边三角形,连接BE,连接DA并延长交CE于点F,交BE于点G,CD=6,EF=2,那么EG的长为__________.

【答案】![]()
【解析】
由等边三角形的性质可得BC=AC,EC=CD=6,∠ACB=∠ECD=60°,由“SAS”可证△ACD≌△BCE,可得∠BEC=∠ADC,EC=DC,根据∠GFE=∠CFD,∠FCD=60°,可得△EGF∽△DCF,则有![]() ,可得
,可得![]() ,设GF=2a,EG=3a,过F作FM⊥EG交EG于M点,在RT△GMF中,利用∠MGF=60°,GF=2a得到GM=a,在RT△EMF中,ME=2a,EF=2,
,设GF=2a,EG=3a,过F作FM⊥EG交EG于M点,在RT△GMF中,利用∠MGF=60°,GF=2a得到GM=a,在RT△EMF中,ME=2a,EF=2,![]() ,由勾股定理得
,由勾股定理得![]()
![]() ,由勾股定理得
,由勾股定理得![]() ,即
,即![]() ,化简求解即可.
,化简求解即可.
解:

∵△ABC和△DCE是等边三角形,
∴BC=AC,EC=CD=6,∠ACB=∠ECD=60°,
∴∠BAE=∠ACD,且BC=AC,EC=CD,
∴△ACD≌△BCE
∴∠BEC=∠ADC,
∵CD=6;EF=2
∴FC=4
又∵∠GFE=∠CFD;∠FCD=60°
∴△EGF∽△DCF
∴∠EGF=∠FCD=60°且
![]() 即
即![]()
∴设GF=2a,EG=3a;
过F作FM⊥EG交EG于M点
在RT△GMF中,∠MGF=60°,GF=2a
∴GM=a,![]()
∴ME=GE-MG=2a
在RT△EMF中,ME=2a,EF=2,![]()
由勾股定理得![]()
即![]() 解得
解得![]()
∴GE=3a=![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
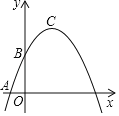
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒冬来临,豆丝飘香,豆丝是鄂州民间传统美食;某企业接到一批豆丝生产任务,约定这批豆丝的出厂价为每千克4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,新工人李明第1天生产100千克豆丝,由于不断熟练,以后每天都比前一天多生产20千克豆丝;设李明第x天(![]() ,且x为整数)生产y千克豆丝,解答下列问题:
,且x为整数)生产y千克豆丝,解答下列问题:

(1)求y与x的关系式,并求出李明第几天生产豆丝280千克?
(2)设第x天生产的每千克豆丝的成本是p元,p与x之间满足如图所示的函数关系;若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据对徐州市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数![]() 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数![]() 的图象如图②所示.
的图象如图②所示.
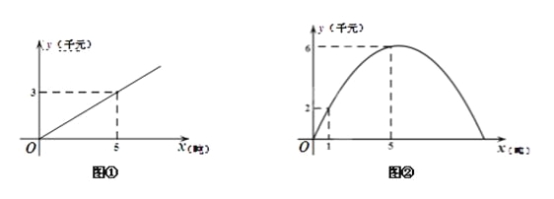
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时 获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,∠C=90°,AC=8,BC=6,
中,∠C=90°,AC=8,BC=6,

(1)若AD是∠BAC的角平分线,AD交BC边于D,过点D作DE⊥AB与点E(如图1),请求出BE的长及![]() 的值;
的值;
(2)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若BC=CF,如图2,请证明
与AC交于点G,若BC=CF,如图2,请证明![]() ∽
∽![]() ;
;
(3)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若
与AC交于点G,若![]() ,如图3,请求出
,如图3,请求出![]() 的值(可以直接利用第(1)题求出的结论)
的值(可以直接利用第(1)题求出的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一直线上,且有一个公共顶点A,若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合,则x的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有相距2km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离为多少千米?(参考数据:![]() ≈1.732,结果保留小数点后一位)
≈1.732,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )
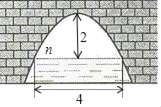
A. 1 m B. 2 m C. 3 m D. 6 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com