
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
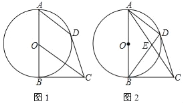
【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,边
是等边三角形,边![]() 上有一点
上有一点![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.

(1)求![]() 的坐标(用含有
的坐标(用含有![]() 的式子表示);
的式子表示);
(2)如图(1),若点![]() 在线段
在线段![]() 上运动,点
上运动,点![]() 在
在![]() 轴的正半轴上运动.当
轴的正半轴上运动.当![]() 的值最小时,
的值最小时,![]() .
.
问:![]() 的面积是否为定值,若是,求其值;若不是,请说明理由.
的面积是否为定值,若是,求其值;若不是,请说明理由.
(3)如图(2),若在![]() 外还有一点
外还有一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 过
过![]() ,
,![]() ,
,![]() 三点,点
三点,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,动点
,动点![]() 在抛物线上.
在抛物线上.

![]() ________,
________,![]() ________,点
________,点![]() 的坐标为________;(直接填写结果)
的坐标为________;(直接填写结果)
![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出所有符合条件的点
为直角边的直角三角形?若存在,求出所有符合条件的点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
![]() 过动点
过动点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线.垂足为
轴的垂线.垂足为![]() ,连接
,连接![]() ,当线段
,当线段![]() 的长度最短时,求出点
的长度最短时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百汇超市服装柜在销售中发现:“七彩”牌童装平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了迎接“元旦”,商场决定采取适降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价
元.为了迎接“元旦”,商场决定采取适降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价![]() 元,那么平均每天就可多售出
元,那么平均每天就可多售出![]() 件.
件.
![]() 如果每件降价
如果每件降价![]() 元,那么平均每天可售出几件?
元,那么平均每天可售出几件?
![]() 要想平均每天销售这种童装上盈利
要想平均每天销售这种童装上盈利![]() 元,那么每件童装应降价多少元?
元,那么每件童装应降价多少元?
![]() 用配方法说明:要想盈利最多,每件童装应降价多少元?
用配方法说明:要想盈利最多,每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=20° ,点A B分别是射线OM、ON上的动点(A、B不与点0重合),若AB![]() OM,在射线ON上有一点C,设∠OAC=x°,下列x的值不能使△ABC为等腰三角形的是( )
OM,在射线ON上有一点C,设∠OAC=x°,下列x的值不能使△ABC为等腰三角形的是( )
A.20
B.45
C.50
D.125
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, △ABC和△CDE均为等腰三角形,AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a,且点A、D、E在同一直线上,连结BE.

(1)求证: AD=BE.
(2)如图2,若a=90°,CM⊥AE于E.若CM=7, BE=10, 试求AB的长.
(3)如图3,若a=120°, CM⊥AE于E, BN⊥AE于N, BN=a, CM=b,直接写出AE的值(用a, b 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
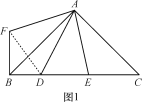
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
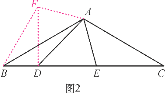
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com