
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD、CM分别是斜边上的高和中线,那么下列结论中错误的是( )
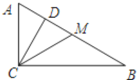
A.CM=ACB.∠ACM=∠DCBC.AD=DMD.DB=4AD
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90° ,AC=BC=4 点D是边AB上的动点(点D与点A、B不重合),过点D作DE⊥AB交射线BC于点E,联结AE,点F是AE的中点,过点D、F作直线,交AC于点G,联结CF、CD.

(1)当点E在边BC上,设DB=![]() , CE=
, CE=![]()
①写出![]() 关于
关于![]() 的函数关系式及定义域;
的函数关系式及定义域;
②判断△CDF的形状,并给出证明;
(2)如果AE=![]() ,求DG的长.
,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=10![]() cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,DE⊥AB,垂足为E,若AC=3,AB=5,则DE的长为______.
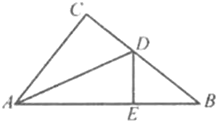
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
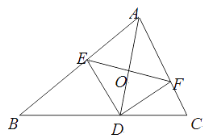
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com