
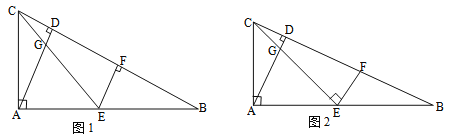
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;
(2)如图2,若AC:AB=1: ![]() ,EF⊥CE,求EF: EG的值.
,EF⊥CE,求EF: EG的值.
【答案】(1)证明见解析;(2)![]()
【解析】(1)根据同角的余角相等得出∠CAD=∠B,根据AC:AB=1:2及点E为AB的中点,得出AC=BE,再利用AAS证明△ACD≌△BEF,即可得出EF=CD;
(2)作EH⊥AD于H,EQ⊥BC于Q,先证明四边形EQDH是矩形,得出∠QEH=90°,则∠FEQ=∠GEH,再由两角对应相等的两三角形相似证明△EFQ∽△EGH,得出EF:EG=EQ:EH,然后在△BEQ中,根据正弦函数的定义得出EQ=![]() BE,在△AEH中,根据余弦函数的定义得出EH=
BE,在△AEH中,根据余弦函数的定义得出EH=![]() AE,又BE=AE,进而求出EF:EG的值.
AE,又BE=AE,进而求出EF:EG的值.
解:(1)证明:如图所示,∵AC:AB=1:2,点E为AB的中点,∴AC=BE,
∵AD⊥BC,∠CAB=90°,
∴∠B+∠BAD=∠DAC+∠BAD=90°,∴∠B=∠DAC ,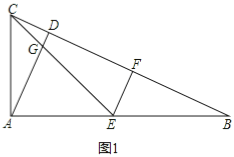
又∵AD⊥BC,EF⊥CB,∴∠ADC=∠BFE=90°,
∴△EFB≌△CDA(AAS)
∴EF=CD.
(2)过点E作EMBD,EN⊥AD,如图2所示,

∵AD⊥BC ∴∠NEM=90° ∵CE⊥EF ∴∠NEG=∠MEF
∵∠ENG=∠EMF=90°,∴△EMF∽△ENG,∴![]() ,
,
∵AD⊥BC,AC:AB=1: ![]() ,∴∠B=30°,∴∠NAE=60°
,∴∠B=30°,∴∠NAE=60°
∴EN=![]() AE,同理可得EM=
AE,同理可得EM=![]() BE,
BE,
∵点E为AB的中点,∴AE=BE,
∴![]() =
=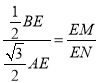 =
=![]() .
.
“点睛”本题考查了相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质,解直角三角形,综合性较强,有一定难度.解题的关键是作辅助线,构造相似三角形,并且证明四边形EQDH是矩形.


科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG; 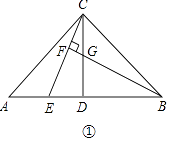
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 , 并说明理由. 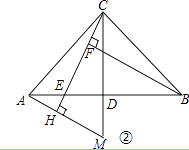
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有13位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设7个获奖名额,某同学知道自己的比赛分数后,要判断自己能否获奖,在这13名同学成绩的统计量中只需知道一个量,它是____.(填“众数”“方差”“中位数”或“平均数”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?
(3)若该专卖店想获得最大利润W,核桃的单价应定为多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是中国的固有领土,位于中国东海,面积约4400000平方米,数据4400000用科学记数法表示为( )
A.44×105
B.4.4×106
C.0.44×107
D.4.4×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com