Question

6．正多边形的内切圆与外接圆的周长之比为$\sqrt{3}$：2，则这个正多边形为（　　）

• A． 正十二边形
• B． 正六边形
• C． 正四边形
• D． 正三角形

Answer 1

分析 设AB是正多边形的一边，OC⊥AB，在直角△AOC中，利用三角函数求得∠AOC的度数，从而求得中心角的度数，然后利用360度除以中心角的度数，即可求得边数．

解答 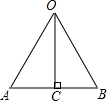解：正多边形的内切圆与外接圆的周长之比为$\sqrt{3}$：2，则半径之比为$\sqrt{3}$：2，
设AB是正多边形的一边，OC⊥AB，
则OC=$\sqrt{3}$，OA=OB=2，
在直角△AOC中，cos∠AOC=$\frac{OC}{AC}$=$\frac{\sqrt{3}}{2}$，
∴∠AOC=30°，
∴∠AOB=60°，
则正多边形边数是：$\frac{360°}{60°}$=6．
故选：B．

点评 本题考查学生对正多边形的概念掌握和计算的能力，正多边形的计算一般是转化成半径，边心距、以及边长的一半这三条线段构成的直角三角形的计算．