练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．已知x2+4x-3=0，求代数式（2x+1）2-（x+2）（x-2）-x（x-4）的值．

    分析 先化简题目中的式子，然后对式子x2+4x-3=0变形，即可解答本题．

    解答 解：（2x+1）2-（x+2）（x-2）-x（x-4）
    =4x2+4x+1-x2+4-x2+4x
    =2x2+8x+5，
    ∵x2+4x-3=0，
    ∴x2+4x=3，
    ∴2x2+8x=6，
    ∴原式=6+5=11．

    点评 本题考查整式的混合运算-化简求值，解答本题的关键是明确整式化简求值的方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

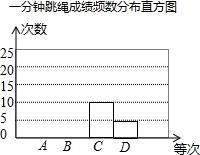    5．今年，合肥市中考体育分数再次增加5分，由去年的50分增加到55分．为备战体育中考，张勇同学就自己平时1分钟跳绳的训练成绩，做了统计，并将训练成绩绘出了如图的频数分布表和频数分布直方图（不完整）（规定：1分钟跳绳120个以下成绩为D等；120-140个为C等；140-160个为B等，160个以上为A等）
    根据以上信息，解答下列问题：
    （1）张勇同学一共记录了50次平时测试的成绩；
    （2）补全频数分布表和频数分布直方图；
    （3）张勇同学从篮球运动、足球运球、掷实心球、坐位体前屈、1分钟跳绳、立定跳远等六个项目中任选两项作为自己的考试项目，求恰好含有1分钟跳绳项目的概率．
    　　 一分钟跳绳成绩分布表
    成绩等次频数（人）频率
    D50.1
    C100.2
    B250.5
    A100.2
    合计501.00

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

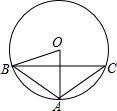    6．如图，⊙O是△ABC的外接圆，∠AOB=60°，AB=AC=4，则弦BC的长为（　　）
    A．2$\sqrt{3}$B．4$\sqrt{3}$C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

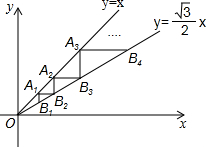    3．如图，点A1（1，1）在直线y=x上，过点A1分别作y轴、x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B1，B2，过点B2作y轴的平行线交直线y=x于点A2，过点A2作x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B3，…，按照此规律进行下去，则点An的横坐标为$（\frac{2\sqrt{3}}{3}）^{n-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解方程组：$\left\{\begin{array}{l}{8x+9y=6①}\\{\frac{4x}{5}+\frac{5y}{6}=\frac{7}{15}②}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2与y轴交于点C（0，4），其中x1，x2是方程x2-4x-12=0的两个根．
    （1）求抛物线的解析式；
    （2）点M是线段AB上的一个动点，过点M作MN∥BC，交AC于点N，连结CM，当△CMN的面积最大时，求点M的坐标；
    （3）点D（4，k）在（1）中抛物线上，点E为抛物线上一动点，在x轴上是否存在点F，使以A、D、E、F为顶点的四边形是平行四边形？如果存在，直接写出所有满足条件的点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）20170+（-$\frac{1}{3}$）-1-3sin60°+$\root{3}{27}$
    （2）（$\frac{1}{a}$-1）÷$\frac{a-1}{{a}^{2}+a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．当x=2时，分式$\frac{x^2-4}{x^2-x-6}$的值为0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列每组数分别是三根小木棒的长度，用它们为边能摆成三角形的是（　　）
    A．1，2，3B．1，3，5C．4，5，6D．3，4，8

    查看答案和解析>>

    同步练习册答案