
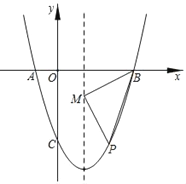
【题目】抛物线的顶点为(1,﹣4),与x轴交于A、B两点,与y轴负半轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)点P为对称轴右侧抛物线上一点,以BP为斜边作等腰直角三角形,直角顶点M落在对称轴上,求P点的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)点P的坐标为(2,﹣3)或(4,5).
【解析】
(1)由抛物线的顶点坐标可设抛物线的解析式为y=a(x-1)2-4,代入点C的坐标可求出a值,进而可得出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点A,B的坐标,设抛物线对称轴与x轴交于点E,过点P作PF∥x轴,交抛物线对称轴于点F,易证△MBE≌△PMF,根据全等三角形的性质可得出ME=PF=x-1,MF=BE=2,进而可得出EF=x+1,结合EF为点P纵坐标的绝对值,即可得出关于x的一元二次方程,解之即可求出x的值,取其大于1的值代入点P的坐标中即可得出结论.
解:(1)设抛物线的解析式为y=a(x﹣1)2﹣4,
将C(0,﹣3)代入y=a(x﹣1)2﹣4,得:﹣3=a(0﹣1)2﹣4,
解得:a=1,
∴抛物线的解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3.
(2)当y=0时,有x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0).
设抛物线对称轴与x轴交于点E,过点P作PF∥x轴,交抛物线对称轴于点F,如图所示.
设点P的坐标为(x,x2﹣2x﹣3)(x>1),则PF=x﹣1,BE=3﹣1=2.
∵∠BME+∠PMF=90°,∠BME+∠MBE=90°,
∴∠MBE=∠PMF.
在△MBE和△PMF中, ,
,
∴△MBE≌△PMF(AAS),
∴ME=PF=x﹣1,MF=BE=2,
∴EF=ME+MF=x+1.
∵EF=|x2﹣2x﹣3|,
∴|x2﹣2x﹣3|=x+1,即x2﹣3x﹣4=0或x2﹣x﹣2=0,
解得:x1=﹣1(舍去),x2=2,x3=4,
∴点P的坐标为(2,﹣3)或(4,5).


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
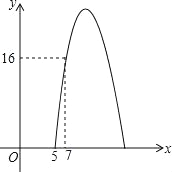
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市对居民生活用水按以下规定收取每月的水费:家庭月用水量如果不超过8吨,按每吨2.5元收费;如果超过8吨,未超过的部分仍按每吨2.5元收取,而超过部分则按每吨4元收取.
(1)设某家庭月用水量为x吨,水费为y元,请写出y与x之间的函数解析式,并在给定的平面直角坐标系中,画出该函数的图象;
(2)如果小明家按题中规定今年3月份应缴水费34元,那么今年3月份小明家用水多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
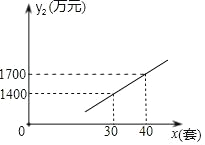
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于80万元,已知这种设备的月产量x(套)与每套的售价y(万元)之间满足关系式y=150﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图象经过点A(﹣1,6).
(m为常数)的图象经过点A(﹣1,6).
(1)求m的值;
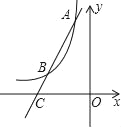
(2)如图,过点A作直线AC与函数y=![]() 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
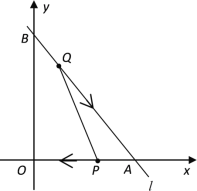
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,且
,且![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,动点
两点,动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒2个单位长度的速度向点
上以每秒2个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 移动,设点P、Q移动的时间为
移动,设点P、Q移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 是以PQ为底的等腰三角形?
是以PQ为底的等腰三角形?
(2)求出点P、Q的坐标;(用含![]() 的式子表达)
的式子表达)
(3)当![]() 为何值时,
为何值时,![]() 的面积是△ABO面积的
的面积是△ABO面积的![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com