
分析 (1)解分式方程求出a的值,解一元一次不等式组求出b的值;
(2)根据方差的计算公式求出这组数据的方差.
解答 解:(1)解方程$\frac{2}{x}$=$\frac{3}{x+3}$得,x=6,即a=6,
解不等式$\left\{\begin{array}{l}{3x-10≥0}\\{9-2x>0}\end{array}\right.$得,$\frac{10}{3}$≤x<$\frac{9}{2}$,整数解为4,即b=4,
则a的值为6,b的值为4,;
(2)$\overline{x}$=$\frac{1}{5}$(9+6+6+4+5)=6,
S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]=$\frac{1}{5}$(9+4+1)=$\frac{14}{5}$.
点评 本题考查的是分式方程的解法、一元一次不等式组的解法和方差的计算,掌握方差的计算公式:方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,图2,正方形网格中每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
如图1,图2,正方形网格中每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
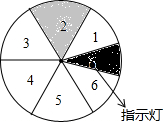 如图,将一个圆盘六等分,并把六个区域分别标上1,2,3,4,5,6,只有区域2为感应区域,中心角为30°的扇形AOB绕点O转动,在其半径OB上装有带指示灯的感应装置,当扇形AOB与区域2有重叠(O点除外)的部分时,指示灯会发光,否则不发光,当扇形ABO任意转动时,指示灯发光的概率为$\frac{1}{4}$.
如图,将一个圆盘六等分,并把六个区域分别标上1,2,3,4,5,6,只有区域2为感应区域,中心角为30°的扇形AOB绕点O转动,在其半径OB上装有带指示灯的感应装置,当扇形AOB与区域2有重叠(O点除外)的部分时,指示灯会发光,否则不发光,当扇形ABO任意转动时,指示灯发光的概率为$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com