
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ��A��B���㣨A��B����ࣩ�����е�B��3��0������y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
��2��������������ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ������ڡ�OBC�ڣ�������OBC�ı߽磩����h��ȡֵ��Χ��
��3�����P��������������x���Ϸ�����һ�㣬��Q��ֱ��l��x=��3�ϣ���PBQ�ܷ��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����ܣ�������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��y=��x2+2x+3��2��2��h��4��3����1��4����0��3��
��������
��1�������ߵĶԳ���x=1��B��3��0����A��B����࣬���ݶ��κ���ͼ������ʿ�֪A��-1��0����
����������y=ax2+bx+c����C��0��3������֪c��ֵ.���A��B��������꣬���ô���ϵ�������a��b��ֵ���ɵ�������L�ı���ʽ��
��2����C��B��������꣬���ô���ϵ�����ɵ�CB��ֱ�߷���.���������䷽�����ɽ�һ��ȷ�������ߵĶ������ꣻͨ������hΪ��ֵʱ�����߶�������BC�ϡ�����OB�ϣ����ܵõ������ߵĶ���������OBC�ڣ�������OBC�ı߽磩ʱh��ȡֵ��Χ.
��3����P��m����m2+2m+3������P��MN��x�ᣬ��ֱ��x=��3��M����B��BN��MN��
ͨ��֤����BNP�ա�PMQ��⼴��.
��1���ѵ�B��3��0������C��0��3������������y=��x2+bx+c�еã���![]()
��ã�![]() ��
��
�������ߵĽ���ʽΪ��y=��x2+2x+3��
��2��y=��x2+2x+3=����x��1��2+4���������ߵĶԳ����ǣ�x=1��
��ԭ�����ߵĶ���ΪD��
�ߵ�B��3��0������C��0��3����
��BC�Ľ���ʽΪ��y=��x+3��
��x=1ʱ��y=2��
��ͼ1���������ߵĶ���D��1��2������ʱ��D���߶�BC�ϣ������ߵĽ���ʽΪ��y=����x��1��2+2=��x2+2x+1��
h=3��1=2��
�������ߵĶ���D��1��0������ʱ��D��x���ϣ������ߵĽ���ʽΪ��y=����x��1��2+0=��x2+2x��1��
h=3+1=4��
��h��ȡֵ��Χ��2��h��4��
��3����P��m����m2+2m+3����
��ͼ2����PQB�ǵ���ֱ�������Σ���PQ=PB��
��P��MN��x�ᣬ��ֱ��x=��3��M����B��BN��MN��
�á�BNP�ա�PMQ��
��BN=PM��
����m2+2m+3=m+3��
��ã�m1=0��ͼ3����m2=1��
��P��1��4����0��3����


 â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ����һ��ֱ�ǵĶ������ڵ�
����һ��ֱ�ǵĶ������ڵ�![]() �����������ŵ�
�����������ŵ�![]() ��ת������ֱ�DZ߷ֱ�����
��ת������ֱ�DZ߷ֱ�����![]() �ڵ�
�ڵ�![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() .
.
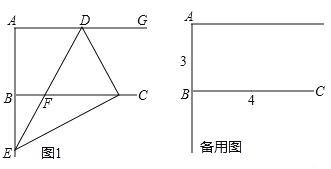
��1����![]() ʱ����
ʱ����![]() �ij���
�ij���
��2����![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ��������
�ĺ�����ϵʽ��������
��3����ת�����У���![]() �����ʱ
�����ʱ![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϵ�һ�����㣨��
�ϵ�һ�����㣨��![]() ���
���![]() ���غϣ�����
���غϣ�����![]() Ϊ��������ֱ��
Ϊ��������ֱ��![]() ������
������![]() .
.
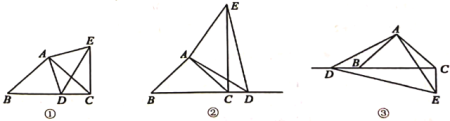
��1����ͼ�٣�����![]() ���߶�
���߶�![]() ��ʱ��ֱ��д��
��ʱ��ֱ��д��![]() ��λ�ù�ϵ���߶�
��λ�ù�ϵ���߶�![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
��2����ͼ�ڣ�����![]() ���߶�
���߶�![]() ���ӳ�����ʱ�����ж��߶�
���ӳ�����ʱ�����ж��߶�![]() ��
��![]() ��λ�ù�ϵ���߶�
��λ�ù�ϵ���߶�![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
��3����ͼ�ۣ�����![]() ���߶�
���߶�![]() ���ӳ�����ʱ�����ж��߶�
���ӳ�����ʱ�����ж��߶�![]() ��λ�ù�ϵ���߶�
��λ�ù�ϵ���߶�![]() ֮���������ϵ����˵������.
֮���������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
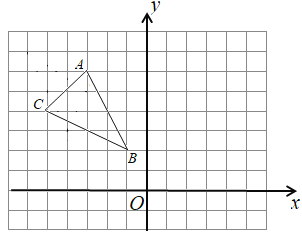
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�����1����֪������![]() ���������������ֱ�Ϊ
���������������ֱ�Ϊ![]() ��
��![]() ��
��![]()
��1������������![]() ����
����![]() ��ԳƵ�������
��ԳƵ�������![]()
��2����![]() ������Ϊ .
������Ϊ .
��3�����������续���߶�![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ��һ���㣬��
��һ���㣬��![]() ����СֵΪ .
����СֵΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������һ�����⣺��ͼ������ֽƬABCD��AB��2��BC��3����Ҫ����ֽƬ��������ƴ��һ����֮�����ȵ������Σ�С�����Ը������������ּ��ķ�������ͼ�٢ڢۢܣ�ͼ��BE��![]() �����м�����ȷ���ǣ�������
�����м�����ȷ���ǣ�������

A.�٢�B.�٢�C.�ڢ�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��![]() x+3��ͼ��ֱ���y�ᣬx�ύ�ڵ�A��B����P�ӵ�B������������BA��ÿ��1����λ���ٶ��˶������P���˶�ʱ��Ϊt�룮
x+3��ͼ��ֱ���y�ᣬx�ύ�ڵ�A��B����P�ӵ�B������������BA��ÿ��1����λ���ٶ��˶������P���˶�ʱ��Ϊt�룮

��1����P���˶������У���ijһʱ�̣���OPA�����Ϊ3�����ʱP�����ꣻ
��2���������˶������У���tΪ��ֵʱ����AOPΪ���������Σ���ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y����![]() x+3��x�ᡢy��ֱ���A��C����OA��OCΪ���ڵ�һ��������������OABC��
x+3��x�ᡢy��ֱ���A��C����OA��OCΪ���ڵ�һ��������������OABC��

��1������ABC��B��D���ۣ�ʹ�õ�A���C�غϣ��ۺ۽�AB�ڵ�D����ֱ��CD�Ľ���ʽ��
��2������x���ϴ��ڵ�P��ʹ��ADPΪ���������Σ�������������ĵ�P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı��� ![]() �����Σ�
�����Σ�![]() B=6���ҡ�ABC=60�� ��M����������һ�㣬����AM��BM��CM����AM+BM+CM ����СֵΪ________��
B=6���ҡ�ABC=60�� ��M����������һ�㣬����AM��BM��CM����AM+BM+CM ����СֵΪ________��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com