
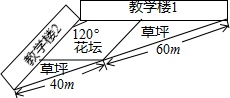
 学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.
学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2. 分析 如图,设菱形AEDF的边长为6k,作BM⊥CA交CA的延长线于M,利用平行线的性质求出BE、CF(用k表示),在RT△ABM中,利用30°性质用k表示AM、BM,在RT△BCM中利用勾股定理求出k即可解决问题.
解答 解:如图,设菱形AEDF的边长为6k,作BM⊥CA交CA的延长线于M.
∵DE∥AC,DF∥AB,
∴$\frac{BE}{AE}$=$\frac{BD}{DC}$=$\frac{40}{60}$=$\frac{2}{3}$,$\frac{FC}{AF}$=$\frac{CD}{BD}$=$\frac{3}{2}$,
∴BE=4k,CF=9k,AB=10k,AC=15k,
在RT△ABM中,∵∠M=90°,AB=10k,∠MAB=60°,
∴∠ABM=30°,
∴AM=$\frac{1}{2}$AB=5k,BM=5$\sqrt{3}$k,
在RT△BCM中,∵BM2+CM2=BC2,
∴75k2+400k2=10000,
∴k=$\frac{20}{\sqrt{19}}$(负根已经舍弃),
∵四边形AEDF是菱形,∠EAF=120°,
∴AE=ED=DF=AF,∠DAE=∠DAF=60°,
∴△AED,△ADF都是等边三角形,
∴S菱形AEDF=2•S△ADE=2×$\frac{\sqrt{3}}{4}$×AE2=$\frac{\sqrt{3}}{2}$×(6×$\frac{20}{\sqrt{19}}$)2=$\frac{7200\sqrt{3}}{19}$.
故答案为$\frac{7200\sqrt{3}}{19}$.
点评 本题考查菱形的性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是添加辅助线,构造直角三角形,利用参数解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2,-1 | B. | -2,1 | C. | -2,-1 | D. | 2,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-x-2=(x-1)(x+2) | B. | -a2+a-$\frac{1}{4}$=$-\frac{1}{4}(2a-1)^{2}$ | ||
| C. | a(x-y)-b(y-x)=(x-y)(a-b) | D. | x2-4+2x=(x+2)(x-2)+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
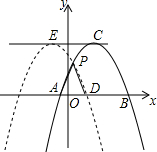 如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.
如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
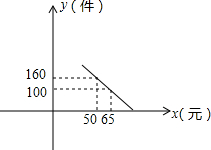 某校两大学生积极响应“自主创业”的号召,准备利用一个月假期投资销售一种进价为每件40元的小家电,通过试管营销发现,当销售单价在40元至100元之间(含40元和100元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数.其图象如图所示.
某校两大学生积极响应“自主创业”的号召,准备利用一个月假期投资销售一种进价为每件40元的小家电,通过试管营销发现,当销售单价在40元至100元之间(含40元和100元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数.其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com