
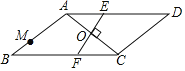
【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为______.
【答案】![]() 或
或![]()
【解析】
设AB=AC=m,根据平行四边形的性质可得OA=OC=![]() AC=
AC=![]() m,继而根据已知解三角形求得FC=
m,继而根据已知解三角形求得FC=![]() m,通过证明△AOE≌△COF,求得AE=FC=
m,通过证明△AOE≌△COF,求得AE=FC=![]() m,从而求得S△AOE=
m,从而求得S△AOE=![]() m2,作AN⊥BC于N,求得BC=
m2,作AN⊥BC于N,求得BC=![]() m,继而求得BF=BC﹣FC=
m,继而求得BF=BC﹣FC=![]() m﹣
m﹣![]() m=
m=![]() m,然后作MH⊥BC于H,分点M为靠近点B的三等分点和靠近点A的三等分点两种情况求出S△BMF的值即可求得答案.
m,然后作MH⊥BC于H,分点M为靠近点B的三等分点和靠近点A的三等分点两种情况求出S△BMF的值即可求得答案.
设AB=AC=m,
∵O是两条对角线的交点,∴OA=OC=![]() AC=
AC=![]() m,
m,
∵∠B=30°,AB=AC,∴∠ACB=∠B=30°,
∵EF⊥AC,∴cos∠ACB=![]() ,即cos30°=
,即cos30°=![]() ,∴FC=
,∴FC=![]() m,
m,
∵AE∥FC,∴∠EAC=∠FCA,又∵∠AOE=∠COF,AO=CO,∴△AOE≌△COF,∴AE=FC=![]() m,
m,
∴OE=![]() AE=
AE=![]() m,∴S△AOE=
m,∴S△AOE=![]() OAOE=
OAOE=![]() ×
×![]() m×
m×![]() m=
m=![]() m2,
m2,
作AN⊥BC于N,
∵AB=AC,∴BN=CN=![]() BC,∵BN=
BC,∵BN=![]() AB=
AB=![]() m,∴BC=
m,∴BC=![]() m,
m,
∴BF=BC﹣FC=![]() m﹣
m﹣![]() m=
m=![]() m,
m,
作MH⊥BC于H,如图1(点M为靠近点B的AB的三等分点),则BM=![]() m,
m,
∵∠B=30°,∴MH=![]() BM=
BM=![]() m,∴S△BMF=
m,∴S△BMF=![]() BFMH=
BFMH=![]() ×
×![]() m×
m×![]() m=
m=![]() m2,
m2,
∴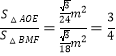 ,
,
如图2(点M为靠近点A的AB的三等分点),则BM=![]() m,
m,
∵∠B=30°,∴MH=![]() BM=
BM=![]() m,∴S△BMF=
m,∴S△BMF=![]() BFMH=
BFMH=![]() ×
×![]() m×
m×![]() m=
m=![]() m2,
m2,
∴ ,
,
故答案为:![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】相传有个人不讲究说话艺术常引起误会,一天他设宴请客,他看到几个人没来,就自言自语:“怎么该来的还不来呢?”客人听了,心想难道我们是不该来的,于是已到的客人的一半走了,他一看十分着急,又说:“嗨,不该走的倒走了!”剩下的人一听,是我们该走啊!又有剩余客人的三分之一离开了,他着急地一拍大腿:“我说的不是他们.”于是剩下的6个人也走了,聪明的你知道最开始来了多少客人吗?( )
A. 16B. 18C. 20D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )

A. 该学校中参与调查的青年教师人数为40人
B. 该学校中青年教师2016年平均每人阅读8本书
C. 该学校中青年教师2016年度看书数量的中位数为4本
D. 该学校中青年教师2016年度看书数量的众数为4本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com