
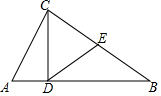
 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
分析 根据直角三角形的性质得到BC=2CE=$\sqrt{3}$,根据勾股定理的逆定理得到∠ACB=90°,根据三角函数的定义得到∠A=60°,求得∠ACD=∠B=30°,得到∠DCE=60°,于是得到结论.
解答 解:∵CD⊥AB,E为BC边的中点,
∴BC=2DE=$\sqrt{3}$,
∵AB=2,AC=1,
∴AC2+BC2=12+($\sqrt{3}$)2=4=22=AB2,
∴∠ACB=90°,
∵tan∠A=$\frac{BC}{AC}$=$\sqrt{3}$,
∴∠A=60°,
∴∠ACD=∠B=30°,
∴∠DCE=60°,
∵DE=CE,
∴∠CDE=60°,
∴∠CDE+∠ACD=90°,
故选C.
点评 本题考查了勾股定理的逆定理,直角三角形的性质,三角函数的定义,熟练掌握勾股定理的逆定理是解题的关键.


科目:初中数学 来源: 题型:解答题
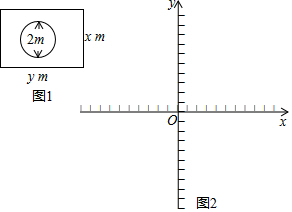 2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.
2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24里 | B. | 12里 | C. | 6里 | D. | 3里 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
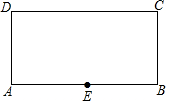 如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.
如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $(\frac{1}{2})^{-2}$=4 | B. | 32×3-1=3 | ||
| C. | 20÷2-2=$\frac{1}{4}$ | D. | (-3×102)3=-2.7×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2m}{{3}^{n}}$ | B. | $\frac{{2}^{m}}{3n}$ | C. | $\frac{2m}{{n}^{3}}$ | D. | $\frac{{m}^{2}}{3n}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 140元 | B. | 150元 | C. | 160元 | D. | 200元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
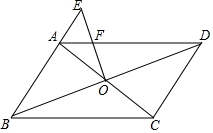 如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=$\frac{16}{9}$.
如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=$\frac{16}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com