
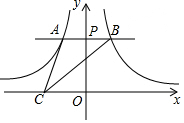
 如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数$y=-\frac{3}{x}$和$y=\frac{1}{x}$的图象交于A点和B点,若点C为x轴上任意一点,连接AC、BC,则△ABC的面积为2.
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数$y=-\frac{3}{x}$和$y=\frac{1}{x}$的图象交于A点和B点,若点C为x轴上任意一点,连接AC、BC,则△ABC的面积为2. 分析 连接OA、OB,根据反比例函数系数与所成三角形面积的关系得:S△BOP=$\frac{1}{2}$×1=$\frac{1}{2}$,S△AOP=$\frac{1}{2}$×3=$\frac{3}{2}$,求出△AOB的面积为2,根据同底等高的两个三角形面积相等得:S△ACB=2.
解答 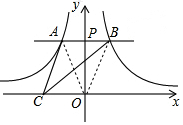 解:连接OA、OB,
解:连接OA、OB,
∵B在反比例函数$y=\frac{1}{x}$上,
∴S△BOP=$\frac{1}{2}$×1=$\frac{1}{2}$,
∵A在反比例函数$y=-\frac{3}{x}$上,
∴S△AOP=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴S△AOB=$\frac{1}{2}$+$\frac{3}{2}$=2,
∵AB∥x轴,
∴S△ABC=S△AOB=2,
故答案为:2.
点评 本题考查了反比例函数比例系数和面积的关系,明确在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
 如图所示,已知直线l的表达式为y=-$\frac{4}{3}$x+8,且l与x轴、y轴分别交于A、B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向A移动,同时动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,其中一点停止运动,另一点也随之停止运动,设点Q、P移动时间为t秒.
如图所示,已知直线l的表达式为y=-$\frac{4}{3}$x+8,且l与x轴、y轴分别交于A、B两点,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向A移动,同时动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,其中一点停止运动,另一点也随之停止运动,设点Q、P移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 |
| 50.5~60.5 | 4 |
| 60.5~70.5 | 8 |
| 70.5~80.5 | 10 |
| 80.5~90.5 | 16 |
| 90.5~100.5 | 12 |
| 合计 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com