
 已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°,得到△DEC.
已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°,得到△DEC.分析 (1)根据平行四边形的判定定理和性质定理判断即可;
(2)根据等底同高的三角形面积相等计算即可;
(3)根据对角线相等的平行四边形是矩形解答即可.
解答 解:(1)由旋转的性质可知,CA=CD,CB=CE,
∴四边形ABDE是平行四边形,
∴AE=BD,AE∥BD;
(2)∵四边形ABDE是平行四边形,
∴△BCD的面积=△DCE的面积=△AEC的面积=△ABC的面积=3cm2,
∴四边形ABDE的面积为12cm2;
(3)当CA=CB时,四边形ABDE为矩形,
∵AD=2AC,BE=2BC,又CA=CB,
∴AD=BE,
∴平行四边形ABDE为矩形.
点评 本题考查的是矩形的判定、平行四边形的判定以及旋转的性质,掌握对角线相等的平行四边形是矩形、对角线互相平分的四边形是平行四边形是解题的关键.


科目:初中数学 来源: 题型:解答题
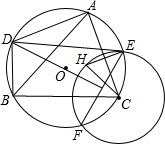 如图,H为△ABC的垂心,圆O为△ABC的外接圆.点E、F为以C为圆心、CH长为半径的圆与圆O的交点,D为线段EF的垂直平分线与圆O的交点.求证:
如图,H为△ABC的垂心,圆O为△ABC的外接圆.点E、F为以C为圆心、CH长为半径的圆与圆O的交点,D为线段EF的垂直平分线与圆O的交点.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).
如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com