Question

1．已知，在平面直角坐标系中，点D的坐标为（a，b），且a，b满足a²-12a+36+$\sqrt{a-b}$=0，E，F分别为x轴，y轴的正半轴上一点，∠EDF=45°．
（1）求a，b的值；
（2）如图1，过E作EG⊥DF于点G，若点E的坐标为（0，2），求点G的坐标；
（3）如图2，过E作EP∥x轴交DF于点P，当E，F运动时，求证：PE+OE+OF=定值．

Answer 1

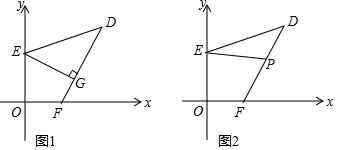
分析 （1）利用非负性的特征即可求出a，b的值，
（2）先判断出△AEG≌△BGD得出AG=BD，OA=BG，即可得出点G的纵横坐标的关系，再用勾股定理即可求出点G的坐标；
（3）构造出如图所示图形，再判断出四边形EFCP为菱形，最后用等量代换即可得出结论．

解答 解：（1）∵a²-12a+36+$\sqrt{a-b}$=0，
∴（a-6）²+$\sqrt{a-b}$=0，
∴a=b=6，
（2）如图1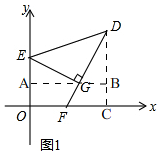，过点D作DC⊥x轴，过点G作AB∥x轴，交y轴于A，
∴∠DBG=90°，
∵∠DGE=90°，
∴EG=DG，∠AGE+∠BGD=90°，
∵∠AGE+∠AEG=90°，
∴∠AEG=∠BGD，
在△AEG和△BGD中，$\left\{\begin{array}{l}{∠EAG=∠GBD}\\{∠AEG=∠BGD}\\{EG=DG}\end{array}\right.$，
∴△AEG≌△BGD，
∴AG=BD，OA=BG，
设G的横坐标为h，则G的纵坐标为6-h，
∴AG=h，OA=6-h，
∵E（0，2），
∴OE=2，
∴AE=OE-OA=2-（6-h）=h-4，
∵D（6，6），E（0，2），
∴DE=2$\sqrt{13}$，
在Rt△DEG中，EG²=$\frac{1}{2}$DE²=26，
在Rt△AEG中，AE²+AG²=EG²，
∴（h-4）²+h²=26，
∴h=-1（舍）或h=5，
∴OA=1，∴G（5，1）；
（3）如图2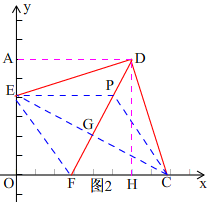，过点D作DA⊥OE，将△ADE绕点D逆时针旋转90°，
而AD=DH=6，所以旋转得到如图2所示的△DHC，
∴DE=DC，∠ADE=∠HDC，
∴∠CDE=90°，
∵∠EDF=45°，
∴∠CDF=45°，
连接CE，
∴DF⊥EC，
∴DF是线段EC的垂直平分线上的点，
∴PE=PC，FE=FC，
∴∠PEC=∠PCE，
∵PE∥x轴，
∴∠PEC=∠OCE=∠PCE，
∵CE⊥PF，
∴CP=CF，
∴PE=EF=CF=PC，
∴四边形PEFC是菱形，
∴PE=CF，
∴PE+OE+OF=CF+OE+OF=OC+OE=OH+CH+OE=OH+AE+OE=OH+OA=6+6=12，
即：PE+OE+OF=定值=12．

点评 此题是三角形综合题，主要考查了非负性，全等三角形的判定和性质，旋转的性质，勾股定理，等腰直角三角形的性质，解本题的关键是判断出△AEG≌△BGD，构造出图形是解本题的难点，是一道很好的中考常考题．