
| 种类 | A选项 | B选项 | C选项 | D选项 | E选项 | F选项 |
| 实施“二孩”的可能变化 | 延缓社会老龄化 | 家庭发展能力提升 | 导致人口暴增 | 增加公共资源压力 | 出生人口性别趋衡 | 劳动年龄人口增加 |
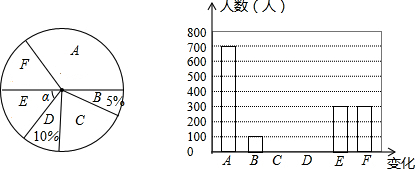
分析 (1)根据B类的有100人,所占的比例是5%,据此即可求得总人数;
(2)利用总人数乘以对应的比例求得D类的人数,再用总人数减去其它各组人数得出C组人数,然后补全统计图;
(3)利用360°乘以E所占的百分比即可求解;
(4)利用样本估计总体的思想,用总人数乘以B选项“家庭发展能力提升”所占的百分比即可.
解答 解:(1)参与调查的市民一共有:700÷35%=2000(人).
故答案为2000;
(2)D的人数:2000×10%=200(人),
C的人数:2000-700-100-200-300-300=400(人).
条形图补充如下: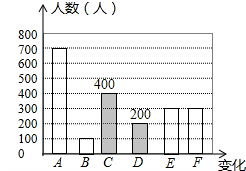
(3)∠α=360°×$\frac{300}{2000}$=54°;
(4)155×5%=7.75(万人).
故估计该区有7.75万人会选择B选项“家庭发展能力提升”.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了用样本估计总体.


科目:初中数学 来源: 题型:解答题
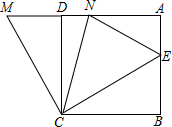 如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CM.
如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
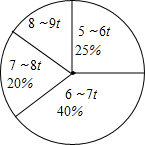 河北新闻网报道,2016年3月29日,石家庄南栗学校各中队开展了以“节约用水”为主题的活动课,该活动课让队员们了解了节水的重要性,丰富了节水知识,某校教导处随机调查了该校200名学生的家庭一个月的用水情况,并将结果进行分组,将分组后的结果绘制成如图所示的扇形统计图(每组含最小值,不含最大值),则调查的学生家庭中一个月用水量为8-9t的家庭有( )
河北新闻网报道,2016年3月29日,石家庄南栗学校各中队开展了以“节约用水”为主题的活动课,该活动课让队员们了解了节水的重要性,丰富了节水知识,某校教导处随机调查了该校200名学生的家庭一个月的用水情况,并将结果进行分组,将分组后的结果绘制成如图所示的扇形统计图(每组含最小值,不含最大值),则调查的学生家庭中一个月用水量为8-9t的家庭有( )| A. | 30户 | B. | 40户 | C. | 50户 | D. | 80户 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | ||
| C. | $\sqrt{{5}^{2}-{3}^{2}}$=$\sqrt{{5}^{2}}$-$\sqrt{{3}^{2}}$=5-3=2 | D. | $\sqrt{3}$-$\sqrt{12}$=-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
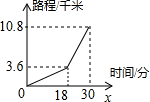 小东早晨从家骑车到学校,先上坡后下坡,行驶的路程y(千米)与所用的时间x(分)之间的函数关系如图所示,若小东返回时上、下坡的速度仍保持不变,则他从学校骑车回家用的时间是42 分.
小东早晨从家骑车到学校,先上坡后下坡,行驶的路程y(千米)与所用的时间x(分)之间的函数关系如图所示,若小东返回时上、下坡的速度仍保持不变,则他从学校骑车回家用的时间是42 分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
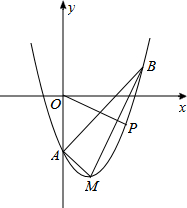 如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com