
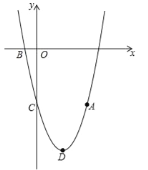
【题目】如图,抛物线![]() (a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)联结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标.
【答案】(1)![]() ;(2)18;(3)E(0,
;(2)18;(3)E(0,![]() ).
).
【解析】
试题分析:(1)先得出C点坐标,再由OC=5BO,得出B点坐标,将A、B两点坐标代入解析式求出a,b;
(2)分别算出△ABC和△ACD的面积,相加即得四边形ABCD的面积;
(3)由∠BEO=∠ABC可知,tan∠BEO=tan∠ABC,过C作AB边上的高CH,利用等面积法求出CH,从而算出tan∠ABC,而BO是已知的,从而利用tan∠BEO=tan∠ABC可求出EO长度,也就求出了E点坐标.
试题解析:(1)∵抛物线![]() 与y轴交于点C,∴C(0,﹣5),∴OC=5.
与y轴交于点C,∴C(0,﹣5),∴OC=5.
∵OC=5OB,∴OB=1,又点B在x轴的负半轴上,∴B(﹣1,0).
∵抛物线经过点A(4,﹣5)和点B(﹣1,0),∴![]() ,解得
,解得![]() ,∴这条抛物线的表达式为
,∴这条抛物线的表达式为![]() ;
;
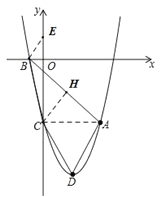
(2)由![]() ,得顶点D的坐标为(2,﹣9).连接AC,∵点A的坐标是(4,﹣5),点C的坐标是(0,﹣5),又S△ABC=
,得顶点D的坐标为(2,﹣9).连接AC,∵点A的坐标是(4,﹣5),点C的坐标是(0,﹣5),又S△ABC=![]() ×4×5=10,S△ACD=
×4×5=10,S△ACD=![]() ×4×4=8,∴S四边形ABCD=S△ABC+S△ACD=18;
×4×4=8,∴S四边形ABCD=S△ABC+S△ACD=18;
(3)过点C作CH⊥AB,垂足为点H.
∵S△ABC=![]() ×AB×CH=10,AB=
×AB×CH=10,AB=![]() ,∴CH=
,∴CH=![]() ,在RT△BCH中,∠BHC=90°,BC=
,在RT△BCH中,∠BHC=90°,BC=![]() ,BH=
,BH=![]() =
=![]() ,∴tan∠CBH=
,∴tan∠CBH=![]() .∵在RT△BOE中,∠BOE=90°,tan∠BEO=
.∵在RT△BOE中,∠BOE=90°,tan∠BEO=![]() ,∵∠BEO=∠ABC,∴
,∵∠BEO=∠ABC,∴![]() =
=![]() ,得EO=
,得EO=![]() ,∴点E的坐标为(0,
,∴点E的坐标为(0,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】春节期间上映的第一部中国科幻电影《流浪地球》,斩获约4 670 000 000元票房,将4 670 000 000用科学记数法表示是( )
A. 4.67×1010B. 0.467×1010C. 0.467×109D. 4.67×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
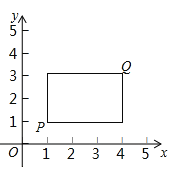
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:

定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016四川省凉山州)阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为a,b,c,记![]() ,那么三角形的面积为
,那么三角形的面积为![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: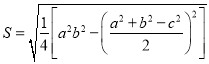 . ②
. ②
下面我们对公式②进行变形: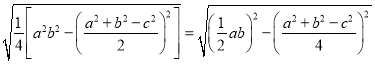
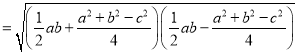
![]()
![]()
![]()
![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
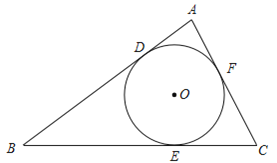
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com