练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    三角形的外角的性质是________；________．

    三角形的一个外角等于与它不相邻的两个内角和    三角形的一个外角大于任何一个与它不相邻的内角
    分析：准确运用语言叙述三角形的外角的性质．
    解答：三角形的外角性质是：三角形的一个外角等于与它不相邻的两个内角和；
    三角形的一个外角大于任何一个与它不相邻的内角．
    点评：本题考查三角形外角的性质的语言叙述，是需要熟记的内容，比较简单．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    27、三角形的外角的性质是
    三角形的一个外角等于与它不相邻的两个内角和
    ；
    三角形的一个外角大于任何一个与它不相邻的内角
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    等腰三角形的性质
    （1）等腰三角形的两个底角
    相等
    相等
    （简称“等边对等角”）．
    （2）等腰三角形的顶角平分线、底边上的
    高
    高
    、底边上的
    中线
    中线
    相互重合．
    （3）等腰三角形是轴对称图形，底边上的中线（顶角平分线、底边上的高）所在直线就是它的
    对称轴
    对称轴
    ．
    （4）等腰三角形两腰上的高、中线分别相等，两底角的平分线也
    相等
    相等
    ．
    （5）等腰三角形一腰上的高与底边的夹角是顶角的
    1
    2
    1
    2
    ．
    （6）等腰三角形顶角的外角平分线平行于这个三角形的
    底边
    底边
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：047

    如图，在△ABC中，∠BAC与∠ABC的平分线AE、BE相交于点E，延长AE交△ABC外接圆于D，连结BD、CD、CE，且∠BDA = 60o.

    求证：△BDE是等边三角形.

    撓旅媸切∨艉托∶鞯慕馓馑悸罚?/P>

    　　他们都用到了三角形的外角与内角的关系，及AE、BE的性质，但小鹏是先证∠DBE=∠DEB；再由∠BDA=60o 得△BDE是等边三角形；小明还用了三角形的内角和，算得∠BED=60o，再由∠BDA=60o 得△BDE是等边三角形.

    王老师的评价是：他们的思路都很好. ?/P>

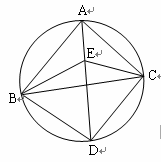
    现请你完成本题的证明，只要求写出一种证法，可参考他们的思路。

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    【考点】菱形的性质；全等三角形的判定与性质；等边三角形的判定与性质．

    【分析】根据菱形的四条边都相等，先判定△ABD是等边三角形，再根据菱形的性质可得∠BDF＝∠C＝60°，再求出DF=CE，然后利用“边角边”即可证明△BDF≌△DCE，从而判定①正确；根据全等三角形对应角相等可得∠DBF＝∠EDC，然后利用三角形的一个外角等于与它不相邻的两个内角的和可以求出∠DMF＝∠BDC＝60°，再根据平角等于180°即可求出∠BMD＝120°，从而判定②正确；根据三角形的一个外角等于与它不相邻的两个内角的和以及平行线的性质求出∠ABM＝∠ADH，再利用“边角边”证明△ABM和△ADH全等，根据全等三角形对应边相等可得AH＝AM，对应角相等可得∠BAM＝∠DAH，然后求出∠MAH＝∠BAD＝60°，从而判定出△AMH是等边三角形，判定出③正确；根据全等三角形的面积相等可得△AMH的面积等于四边形ABMD的面积，然后判定出④错误．

    【解答】在菱形ABCD中，∵AB＝BD，

    ∴AB＝BD＝AD，

    ∴△ABD是等边三角形，

    ∴根据菱形的性质可得∠BDF＝∠C＝60°，

    ∵BE＝CF，

    ∴BC－BE＝CD－CF，

    即CE＝DF，

    在△BDF和△DCE中，CE＝DF；∠BDF＝∠C＝60°；BD＝CD，

    ∴△BDF≌△DCE（SAS），故①小题正确；

    ∴∠DBF＝∠EDC，

    ∵∠DMF＝∠DBF＋∠BDE＝∠EDC＋∠BDE＝∠BDC＝60°，

    ∴∠BMD＝180°－∠DMF＝180°－60°＝120°，故②小题正确；

    ∵∠DEB＝∠EDC＋∠C＝∠EDC＋60°，∠ABM＝∠ABD＋∠DBF＝∠DBF＋60°，

    ∴∠DEB＝∠ABM，

    又∵AD∥BC，

    ∴∠ADH＝∠DEB，

    ∴∠ADH＝∠ABM，

    在△ABM和△ADH中，AB＝AD；∠ADH＝∠ABM；DH＝BM，

    ∴△ABM≌△ADH（SAS），

    ∴AH＝AM，∠BAM＝∠DAH，

    ∴∠MAH＝∠MAD＋∠DAH＝∠MAD＋∠BAM＝∠BAD＝60°，

    ∴△AMH是等边三角形，故③小题正确；

    ∵△ABM≌△ADH，

    ∴△AMH的面积等于四边形ABMD的面积，

    又∵△AMH的面积＝AM·AM＝AM2，

    ∴S四边形ABMD＝AM2，S四边形ABCD≠S四边形ABMD，故④小题错误，

    综上所述，正确的是①②③共3个．

    故选C．

    【点评】本题考查了菱形的性质，全等三角形的判定与性质，等边三角形的判定与性质，题目较为复杂，特别是图形的识别有难度，从图形中准确确定出全等三角形并找出全等的条件是解题的关键．

    查看答案和解析>>

    同步练习册答案