练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

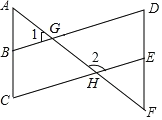
    【题目】如图，已知AF分别与BD、CE交于点G、H，其中∠1＋∠2=180°.

    （1）判断BD和CE有怎样的位置关系，并说明理由；

    （2）若∠A=∠F，探索∠C与∠D的数量关系，并证明你的结论.

    【答案】（1）BD∥CE，理由见解析；（2），理由见解析；

    【解析】

    （1）根据对顶角相等得出∠DGH=∠1，再由平行线的判定定理即可得出结论；
    （2）先根据BD∥CE得出∠D=∠CEF，再由∠A=∠F得出AC∥DF，据此可得出结论．

    （1）证明：∵∠1=∠DGH，∠1＋∠2=180°，

    ∴∠DGH+∠2=180°，

    ∴BD∥CE；

    （2）∠C=∠D．

    理由：∵BD∥CE，

    ∴∠D=∠CEF．

    ∵∠A=∠F，

    ∴AC∥DF，

    ∴∠C=∠CEF，

    ∴∠C=∠D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了解某种车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来， 制成如表：

    汽车行驶时间 t（小时）

    0

    1

    2

    3

    …

    油箱剩余油量 Q（升）

    100

    94

    88

    82

    …

    （1）上表反映的两个变量中，自变量是 ，因变量是 ；

    （2）根据上表可知，该车油箱的大小为 升，每小时耗油 升；

    （3）请求出两个变量之间的关系式（用 t 来表示 Q）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.

    （发现与证明）中，，将沿翻折至，连结.

    结论1：与重叠部分的图形是等腰三角形；

    结论2：.

    试证明以上结论.

    （应用与探究）

    在中，已知，，将沿翻折至，连结.若以、、、为顶点的四边形是正方形，求的长.（要求画出图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD与⊙O交于点C，OC平分∠AOB，∠B=60°．

    （1）求证：AM是⊙O的切线；

    （2）若DC=2，求图中阴影部分的面积．（结果保留π和根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律，称之为“杨辉三角”，这个三角形给出了(a+b)n (n=1，2，3，4，…)的展开式的系数规律(按n的次数由大到小的顺序)：

    1 1 (a+b)1=a+b

    1 2 1 (a+b)2=a2+2ab+b2

    1 3 3 1 (a+b)3=a3+3a2b+3ab2+b3

    1 4 6 4 1 (a+b)4=a4+4a3b+6a2b2+4ab3+b4

    …… ……

    请依据上述规律，写出(x1)2019展开式中含x2018项的系数是________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人(不设弃权票)，选出了票数最多的甲、乙、丙三人.投票结果统计如图一：

    其次，对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示：

    测试项目

    测试成绩/分

    甲

    乙

    丙

    笔试

    92

    90

    95

    面试

    85

    95

    80

    图二是某同学根据上表绘制的一个不完全的条形图.

    请你根据以上信息解答下列问题：

    (1)补全图一和图二；

    (2)请计算每名候选人的得票数；

    (3)若每名候选人得一票记1分，投票、笔试、面试三项得分按照2:5:3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明为了测量楼房AB的高度，他从楼底的B处沿着斜坡向上行走20m，到达坡顶D处．已知斜坡的坡角为15°．（以下计算结果精确到0.1m）

    （1）求小明此时与地面的垂直距离CD的值；

    （2）小明的身高ED是1.6m，他站在坡顶看楼顶A处的仰角为45°，求楼房AB的高度．（sin15°≈0.2588，cos15°≈0.9659 ，tan≈.0.2677 )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学活动课上，同学们探究了角平分线的作法．下面给出三个同学的作法：

    小红的作法

    如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再过点O作MN的垂线，垂足为P，则射线OP便是∠AOB的平分线．

    小明的作法

    如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．

    小刚的作法

    如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，则射线OP便是∠AOB的平分线．

    请根据以上情境，解决下列问题

    (1)小红的作法依据是 ．

    (2)为说明小明作法是正确的，请帮助他完成证明过程．

    证明：∵OM＝ON，OC＝OC， ，

    ∴△OMC≌△ONC( )(填推理的依据)

    (3)小刚的作法正确吗?请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连结AM、BM．

    （1）求抛物线的函数关系式；

    （2）判断△ABM的形状，并说明理由；

    （3）把抛物线与直线y=x的交点称为抛物线的不动点．若将（1）中抛物线平移，使其顶点为（m，2m），当m满足什么条件时，平移后的抛物线总有不动点．

    查看答案和解析>>

    同步练习册答案