
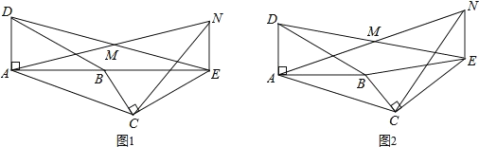
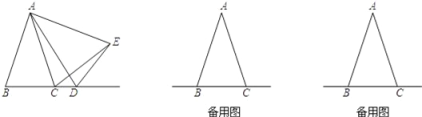
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
【答案】(1)①见解析,②AC=CN,见解析;(2)△BCE绕点B逆时针旋转一周,旋转过程中△CAN为等腰直角三角形时,旋转角度为60°或240°.
【解析】
(1)①先判断出BC=AD,EC=AB,再判断出∠MEN=∠MDA,即可得出结论;②首先证明△MEN≌△MDA,得BC=EN;然后证明△ABC≌△CEN,得到AC=CN;
(2)首先证明△MEN≌△MDA,得BC=EN;然后证明△ABC≌△CEN,得到AC=CN,再判断出∠ACB=90°,进而判断出∠BAC=∠ACB,再由BA≠CB,得出点A,B,C在同一条直线上,即可得出结论.
解:(1)①∵△BAD≌△BCE,
∴BC=AD,EC=AB.
∵EN∥AD,
∴∠MEN=∠MDA.
在△MEN与△MDA中,
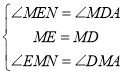
∴△MEN≌△MDA(ASA),
②AC=CN,
由①知,△MEN≌△MDA,
∴EN=AD,
∴EN=BC.
在△ABC与△CEN中,
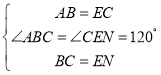
∴△ABC≌△CEN(SAS),
∴AC=CN.
(2)与(1)同理,可证明△MEN≌△MDA,
∴EN=BC.
设旋转角为α,则∠ABC=120°+α,
∠DBE=360°-∠DBA-∠ABC-∠CBE=360°-30°-(120°+α)-60°=150°-α.
∵BD=BE,
![]() ,
,
∵EN∥AD,
∴∠MEN=∠MDA=∠ADB+∠BDE=![]() ,
,
![]() ,
,
∴∠ABC=∠CEN.
在△ABC与△CEN中,
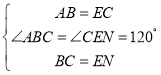 ,
,
∴△ABC≌△CEN(SAS),
∴AC=CN,∠BAC=∠NCE,
∵△CAN能成为等腰直角三角形
∴∠ACN=90°,
∴∠ACB=∠NCE,
∴∠BAC=∠ACB,
∵AB≠CB,
∴点A,B,C在同一条直线上,
此时旋转角为60°.如下图所示:
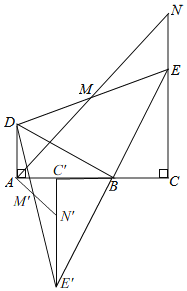
即△BCE绕点B逆时针旋转一周,旋转过程中△CAN为等腰直角三角形时,旋转角度为60°或240°.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
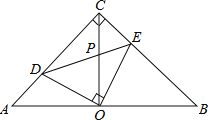
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成丁一个大的正方形(如图1),这个矩形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2,称为勾股定理.
证明:∵大正方形面积表示为S=c2,,又可表示为S=4×![]() ab+(b-a)2,
ab+(b-a)2,
∴4×![]() ab+(b-a)2=c2.
ab+(b-a)2=c2.
∴______________
即直角三角形两直角边的平方和等于斜边的平方.
(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论,请你帮助小明完成验证的过程.
(3)如图3所示,∠ABC=∠ACE=90°,请你添加适当的辅助线,证明结论a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
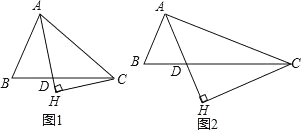
【题目】已知△ABC 中,AD 是∠BAC 的平分线,且 AD=AB,过点 C 作 AD 的垂线,交 AD 的延长线于点 H.
(1)如图 1,若∠BAC=60°.
①直接写出∠B 和∠ACB 的度数;
②若 AB=2,求 AC 和 AH 的长;
(2)如图 2,用等式表示线段 AH 与 AB+AC 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴,交直线
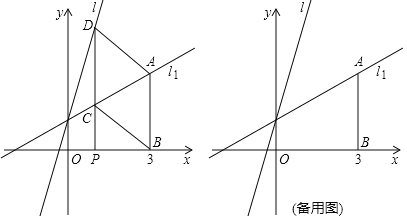
轴,交直线![]() 于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与
于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与![]() 、
、![]() 交于点C、D,连接AD、BC.
交于点C、D,连接AD、BC.
![]() 直接写出线段
直接写出线段![]() ______;
______;
![]() 当P的坐标是
当P的坐标是![]() 时,求直线BC的解析式;
时,求直线BC的解析式;
![]() 若
若![]() 的面积与
的面积与![]() 的面积相等,求点P的坐标.
的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com