
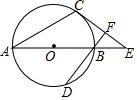
 如图,AB是⊙O的直径,AC是⊙O的弦,E是AB延长线上的点,BF⊥EC于F交⊙O于D,∠EBF=2∠EAC.
如图,AB是⊙O的直径,AC是⊙O的弦,E是AB延长线上的点,BF⊥EC于F交⊙O于D,∠EBF=2∠EAC.分析 (1)欲证明CE是⊙O的切线,只要证明OC⊥EC,只要证明OC∥BF即可;
(2)由Rt△OCE∽Rt△BDA,可得$\frac{OC}{OE}$=$\frac{BD}{AB}$=$\frac{2}{3}$,设⊙O的半径为2r,OE=3r,BE=r,由Rt△EBF∽Rt△ABD,可得$\frac{BF}{BD}$=$\frac{BE}{AB}$=$\frac{1}{4}$;
解答 (1)证明:连结OC.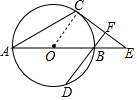
∵OA=OC,
∴∠EAC=∠OCA,
∴∠COE=∠EAC+∠OCA=2∠EAC,
∵∠EBF=2∠EAC,
∴∠COE=∠FBE,
∴OC∥BF,
∵BF⊥CE,
∴OC⊥CE,
∴PC是⊙O的切线.
(2)解:由Rt△OCE∽Rt△BDA,可得$\frac{OC}{OE}$=$\frac{BD}{AB}$=$\frac{2}{3}$,
设⊙O的半径为2r,OE=3r,BE=r,
∵Rt△EBF∽Rt△ABD,
∴$\frac{BF}{BD}$=$\frac{BE}{AB}$=$\frac{1}{4}$.
点评 本题考查切线的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
 某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:| 时间x(秒) | 0 | 1 | 2 | 2.5 | 3 | … |
| 速度v(米/秒) | 8 | 6 | 4 | 3 | 2 | … |
| 时间x(秒) | 0 | 1 | 2 | 3 | … |
| 距离s(米) | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
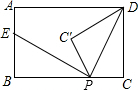 如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:
如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
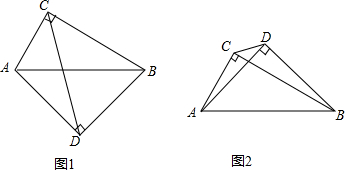
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
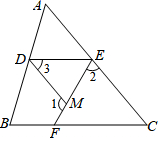 如图,在三角形ABC中,D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠2-∠1=30°.
如图,在三角形ABC中,D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠2-∠1=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com