
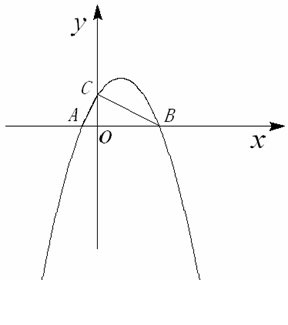
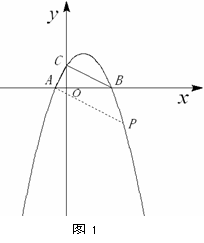
如图,二次函数 的图象与
的图象与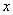 轴交于
轴交于 ,
,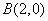 两点,且与
两点,且与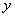 轴交于点
轴交于点 .
.
(1)求该抛物线的解析式,并判断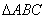 的形状;
的形状;
(2)在此抛物线上是否存在点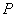 ,使得以
,使得以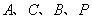
四点为顶点的四边形是直角梯形?若存在,求出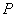 点的坐标;
点的坐标;
若不存在,说明理由.
解:根据题意,将A( ,0),B(2,0)代入y=-x2+ax+b中,
,0),B(2,0)代入y=-x2+ax+b中,
得 解之,得
解之,得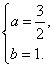 全所以抛物线的解析式为y=-x2+
全所以抛物线的解析式为y=-x2+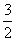 x+1.
x+1.
当x=0时,y=1.所以点C的坐标为(0,1)。
所以在△AOC中,AC=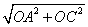 =
=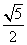 .
.
在△BOC中,BC= =
=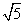 .
.
 AB=OA+OB=
AB=OA+OB=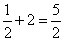 .
.
因为AC2+BC2=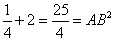 .
.
所以△ABC是直角三角形。 
(2)存在。
由(1)知,AC⊥BC,
① 若以BC为底边,则BC∥AP,如图(1)所示,
可求得直线BC的解析式为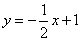 .
.
直线AP可以看作是由直线AC平移得到的,
所以设直线AP的解析式为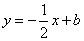 ,
,
将A( ,0)代入直线AP的解析式求得b=
,0)代入直线AP的解析式求得b=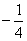 ,
,
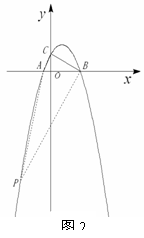 所以直线AP的解析式为
所以直线AP的解析式为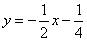 .
.
因为点P既在抛物线上,又在直线AP上,
所以点P的纵坐标相等,即-x2+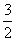 x+1=
x+1=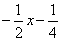 .
.
解得 (不合题意,舍去).
(不合题意,舍去).
当x=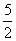 时,y=
时,y= .
.
所以点P的坐标为(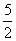 ,
, ).
).
② 若以AC为底边,则BP∥AC,如图(2)所示,
可求得直线AC的解析式为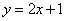 .
.
直线BP可以看作是由直线AC平移得到的,所以设直线BP的解析式为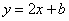 ,
,
将B(2,0)代入直线BP的解析式求得b=-4,所以直线BP的解析式为y=2x-4.
因为点P既在抛物线上,又在直线BP上,所以点P的纵坐标相等,即-x2+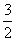 x+1=2x-4
x+1=2x-4
解得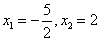 (不合题意,舍去).
(不合题意,舍去).
当x=-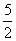 时,y=-9.所以点P的坐标为(-
时,y=-9.所以点P的坐标为(-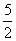 ,-9).
,-9).
综上所述,满足条件的点P的坐标为(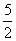 ,
, )或(-
)或(-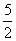 ,-9)
,-9)


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出了300元以后,超出部分按原价8折优惠;在乙超市累计购买商品超 出200元之后,超出部分按原价8
出200元之后,超出部分按原价8 .5折优惠,设顾客预计累计购物x元(x>300)(8分)
.5折优惠,设顾客预计累计购物x元(x>300)(8分)
(1)当x =400元时,到哪家超市购物优惠。
(2)当x为何值时,两家 超市购物所花实际钱数相同。
超市购物所花实际钱数相同。
查看答案和解析>>
科目:初中数学 来源: 题型:
某校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分 四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.

[来源:学|科|网Z|X|X|K]
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该课题研究小组共抽查了__________名同学的体育测试成绩;扇形统计图中B级所占的百分比b=___________,D级所在小扇形的圆心角的大小为 ;
(2)请直接补全条形统计图;
(3)若该校九年级共有600名同学,请估计该校九年级同学体育测试达标(测试成绩 级以上,含
级以上,含 级)的人数.
级)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列分解因式的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3.
(1)上述分解因式的方法是_______,共应用了_________次;
(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2 012,则需应用上述方法_____次,其结果是_____;
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n为正整数)=_______ .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com