
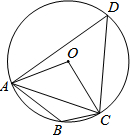
 如图,四边形ABCD内接于⊙O,∠OAC=40°,求∠ABC的度数.
如图,四边形ABCD内接于⊙O,∠OAC=40°,求∠ABC的度数.  Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE.当△ABC满足什么条件时,四边形BECD是正方形.
在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE.当△ABC满足什么条件时,四边形BECD是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
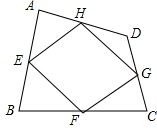 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com