
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 是
是![]() 上一动点,则
上一动点,则![]() 的最大值为__________.
的最大值为__________.
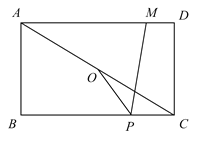
【答案】![]()
【解析】
连接MO并延长交BC于P,则此时,PMPO的值最大,且PMPO的最大值=OM,根据全等三角形的性质得到AM=CP=4,OM=OP,求得PB=1,过M作MN⊥BC于N,得到四边形MNCD是矩形,得到MN=CD,CN=DM,根据勾股定理即可得到结论.
∵在矩形ABCD中,AD=5,MD=1,
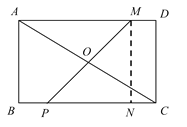
∴AM=ADDM=51=4,
连接MO并延长交BC于P,
则此时,PMPO的值最大,且PMPO的最大值=OM,
∵AM∥CP,
∴∠MAO=∠PCO,
∵∠AOM=∠COP,AO=CO,
∴△AOM≌△COP(ASA),
∴AM=CP=4,OM=OP,
∴PB=54=1,
过M作MN⊥BC于N,
∴四边形MNCD是矩形,
∴MN=CD=AB=4,CN=DM=1,
∴PN=511=3,
∴MP=![]() =
=![]() =5,
=5,
∴OM=![]() MP=
MP=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2和x轴交于A,B(点A在点B右边)两点,和y轴交于点C,P为抛物线上的动点.
(1)求出A,C的坐标;
(2)求动点P到原点O的距离的最小值,并求此时点P的坐标;
(3)当点P在x轴下方的抛物线上运动时,过P的直线交x轴于E,若△POE和△POC全等,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
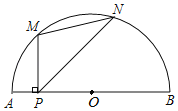
【题目】如图,P是半圆O中![]() 所对弦AB上一动点,过点P作PM⊥AB交
所对弦AB上一动点,过点P作PM⊥AB交![]() 于点M,作射线PN交
于点M,作射线PN交![]() 于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
小超根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4.2 | 2.9 | 2.6 | 2.0 | 1.6 | 0 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当MN=2AP时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
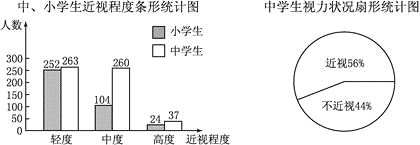
【题目】某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图.(近视程度分为轻度、中度、高度三种)
(1)求这1000名小学生患近视的百分比.
(2)求本次抽查的中学生人数.
(3)该市有中学生8万人,小学生10万人.分别估计该市的中学生与小学生患“中度近视”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(1,t+1),B(t-5,-1)两点.
的图象交于A(1,t+1),B(t-5,-1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=![]() 图象上任意两点,且满足c=n+1时,求
图象上任意两点,且满足c=n+1时,求![]() 的值.
的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<-3,0<x2<1,当x1x2=-3时,判断四边形NFEM的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() (
(![]() ,1)为函数
,1)为函数![]() (
(![]() ,
,![]() 为常数,且
为常数,且![]() )与
)与![]() 的图象的交点.
的图象的交点.
(1)求![]() ;
;
(2)若函数![]() 的图象与
的图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() ,
,![]() ;
;
(3)若![]() ,设当
,设当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
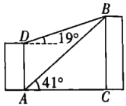
【题目】如图,已知一居民楼![]() 前方
前方![]() 处有一建筑物
处有一建筑物![]() ,小敏在居民楼的顶部
,小敏在居民楼的顶部![]() 处和底部
处和底部![]() 处分别测得建筑物顶部
处分别测得建筑物顶部![]() 的仰角为
的仰角为![]() 和
和![]() ,求居民楼的高度
,求居民楼的高度![]() 和建筑物的高度
和建筑物的高度![]() (结果取整数).
(结果取整数).
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
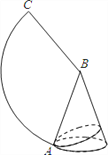
【题目】如图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体考时间越来越近,年级想了解初三年级1000名学生周末在家体育锻炼的情况,在初三年级随机抽取了20名男生和20名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了以下数据(单位:min):
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
统计数据,并制作了如下统计表:
时间 x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 | |
男生 | 2 | 8 | 8 | 2 | |
女生 | 1 | m | n | 3 |
分析数据:两组数据的极差、平均数、中位数、众数如下表所示
极差 | 平均数 | 中位数 | 众数 | |
男生 | a | 65.75 | b | 90 |
女生 | c | 75.5 | 75 | d |
(1)请将上面的表格补充完整:m= ,n= ,a= ,b= ,c= ,d=
(2)已知该年级男女生人数差不多,根据调查的数据,估计初三年级周末在家锻炼的时间在 90min 以上的同学约有多少人?
(3)李老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持李老师观点的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com