
我国宋代数学家杨辉在1261年提到一个有意思的关于 展开式中各项系数间的关系:
展开式中各项系数间的关系:
 ,它只有一项,系数为1;
,它只有一项,系数为1; ,它有两项,系数为1、1;
,它有两项,系数为1、1; ,它有三项,系数为1、2、1;
,它有三项,系数为1、2、1; ,它有四项,系数为1、3、3、1;
,它有四项,系数为1、3、3、1;
如果把其系数按上图排列,得到一个三角形,我们把它叫杨辉三角,其规律的发现比欧洲早393年;那么 展开项的所有系数的和为 ( )
展开项的所有系数的和为 ( )
| A.16 | B.22 | C.32 | D.64 |
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源:2015届河南省郑州市七年级下学期期中考试数学试卷(解析版) 题型:选择题
我国宋代数学家杨辉在1261年提到一个有意思的关于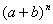 展开式中各项系数间的关系:
展开式中各项系数间的关系:

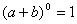 ,它只有一项,系数为1;
,它只有一项,系数为1;
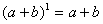 ,它有两项,系数为1、1;
,它有两项,系数为1、1;
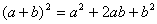 ,它有三项,系数为1、2、1;
,它有三项,系数为1、2、1;
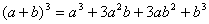 ,它有四项,系数为1、3、3、1;
,它有四项,系数为1、3、3、1;
如果把其系数按上图排列,得到一个三角形,我们把它叫杨辉三角,其规律的发现比欧洲早393年;那么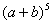 展开项的所有系数的和为 ( )
展开项的所有系数的和为 ( )
A.16 B.22 C.32 D.64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com