
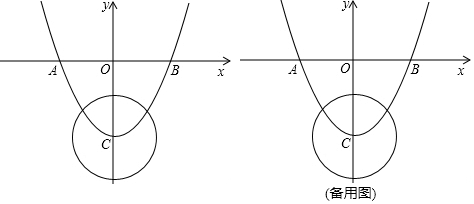
分析 (1)在抛物线解析式中令y=0可求得B点坐标,令x=0可求得C点坐标;
(2)①当PB与⊙相切时,△PBC为直角三角形,如图1,连接BC,根据勾股定理得到BC=5,BP2=2$\sqrt{5}$,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到$\frac{{P}_{2}F}{{P}_{2}E}$=$\frac{C{P}_{2}}{B{P}_{2}}$=2,设OC=P2E=2x,CP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=$\frac{11}{5}$,EP2=$\frac{22}{5}$,求得P2($\frac{11}{5}$,-$\frac{22}{5}$),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
(3)如图3中,连接AP,∵OB=OA,BE=EP,推出OE=$\frac{1}{2}$AP,可知当AP最大时,OE的值最大,
解答 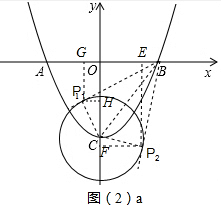 解:(1)在y=$\frac{4}{9}$x2-4中,令y=0,则x=±3,令x=0,则y=-4,
解:(1)在y=$\frac{4}{9}$x2-4中,令y=0,则x=±3,令x=0,则y=-4,
∴B(3,0),C(0,-4);
故答案为:3,0;0,-4;
(2)存在点P,使得△PBC为直角三角形,
①当PB与⊙相切时,△PBC为直角三角形,如图(2)a,
连接BC,
∵OB=3.OC=4,
∴BC=5,
∵CP2⊥BP2,CP2=$\sqrt{5}$,
∴BP2=2$\sqrt{5}$,
过P2作P2E⊥x轴于E,P2F⊥y轴于F,
则△CP2F∽△BP2E,四边形OCP2B是矩形,
∴$\frac{{P}_{2}F}{{P}_{2}E}$=$\frac{C{P}_{2}}{B{P}_{2}}$=$\frac{1}{2}$,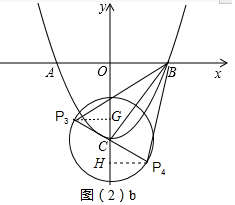
设OC=P2E=2x,CP2=OE=x,
∴BE=3-x,CF=2x-4,
∴$\frac{BE}{CF}$=$\frac{3-x}{2x-4}$=2,
∴x=$\frac{11}{5}$,2x=$\frac{22}{5}$,
∴FP2=$\frac{11}{5}$,EP2=$\frac{22}{5}$,
∴P2($\frac{11}{5}$,-$\frac{22}{5}$),
过P1作P1G⊥x轴于G,P1H⊥y轴于H,
同理求得P1(-1,-2),
②当BC⊥PC时,△PBC为直角三角形,
过P4作P4H⊥y轴于H,
则△BOC∽△CHP4,
∴$\frac{CH}{OB}=\frac{{P}_{4}H}{OC}$=$\frac{{P}_{4}C}{BC}$=$\frac{\sqrt{5}}{5}$,
∴CH=$\frac{3\sqrt{5}}{5}$,P4H=$\frac{4\sqrt{5}}{5}$,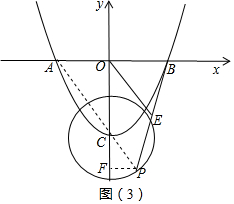
∴P4($\frac{4\sqrt{5}}{5}$,-$\frac{3\sqrt{5}}{5}$-4);
同理P3(-$\frac{4\sqrt{5}}{5}$,$\frac{3\sqrt{5}}{5}$-4);
综上所述:点P的坐标为:(-1,-2)或($\frac{11}{5}$,-$\frac{22}{5}$)或($\frac{4\sqrt{5}}{5}$,-$\frac{3\sqrt{5}}{5}$-4)或(-$\frac{4\sqrt{5}}{5}$,$\frac{3\sqrt{5}}{5}$-4);
(3)如图(3),连接AP,∵OB=OA,BE=EP,
∴OE=$\frac{1}{2}$AP,
∴当AP最大时,OE的值最大,
∵当P在AC的延长线上时,AP的值最大,最大值=5+$\sqrt{5}$,
∴OE的最大值为$\frac{5+\sqrt{5}}{2}$
故答案为:$\frac{5+\sqrt{5}}{2}$.
点评 本题考查了根据函数的解析式求得点的坐标,圆与直线是位置关系,勾股定理,相似三角形的判定和性质,考查中位线和圆外一定点到圆上距离的最值 等知识点,正确的作出辅助线是解题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | 平均数为160 | B. | 中位数为158 | C. | 众数为158 | D. | 方差为20.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
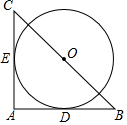 如图,在Rt△ABC中,∠A=90°,BC=2$\sqrt{2}$,以BC的中点O为圆心分别与AB,AC相切于D,E两点,则$\widehat{DE}$的长为( )
如图,在Rt△ABC中,∠A=90°,BC=2$\sqrt{2}$,以BC的中点O为圆心分别与AB,AC相切于D,E两点,则$\widehat{DE}$的长为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 地区 | A | B | C | D | E | F | G | H | I |
| 万册 | 28 | 24 | 23 | 14 | 16 | 15 | 5 |
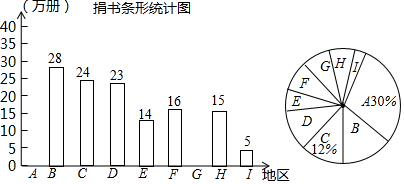
| A. | 捐书的总数为200万册 | |
| B. | 捐书数据的中位数是16万册 | |
| C. | 捐书数据的众数是60万册 | |
| D. | 捐书数扇形统计图中表示G的扇形的圆心角为30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )| A. | x-y2=3 | B. | 2x-y2=9 | C. | 3x-y2=15 | D. | 4x-y2=21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
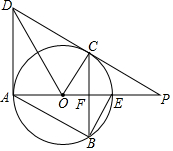 如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.
如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
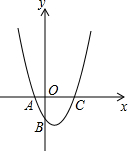 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.
如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:解答题
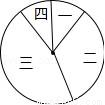
某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com