
【题目】如图,用棱长为a的小正方体拼成长方体,按照这样的拼法,第n个长方体表面积是_____.

【答案】(4n+6)a2
【解析】
棱长为1厘米的正方体的一个面的面积是1平方厘米, 且相邻的2个正方体拼组在一起减少了2个小正方体的面:
第一个长方体的表面积是: 10个小正方形的面, 可以写成1![]() 4+6;
4+6;
第二个长方体的表面积是: 14个小正方形的面, 可以写成2![]() 4+6;
4+6;
第三个长方体的表面积是: 18个小正方形的面, 可以写成3![]() 4+6…;.
4+6…;.
则第n个长方体的表面积是: 4n+6个小正方形的面积
根据题干分析可得: 第n个长方体的表面积是: 4n+6个小正方形的面积;
小正方体的一个面的面积为:a![]() a=
a=![]() ,
,
所以第n个长方体的表面积为:[(n+1)![]() 4+2]
4+2] ![]() =(4n+6)
=(4n+6) ![]() .
.
故答案为: (4n+6)a2.


科目:初中数学 来源: 题型:
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)OA可能在∠BOD的内部,也可能在∠BOD的外部,请分两种情况,在下图中用直尺、量角器画出射线OD,ON的准确位置;
(2)当α=40°时,求(1)中∠MON的度数,要求写出计算过程;
(3)用含α的代数式表示∠MON的度数.(直接写出结果即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的网格称之为三角形网格,它的每一个小三角形都是边长为1的正三角形,画出格点△ABC(即△ABC三个顶点都在小正三角形的顶点处),如图所示,请按照下列要求,画出相应的图形,并计算. 
(1)请在①中画出一个与△ABC面积相等,且不全等的格点三角形,并写出相应的面积; 
(2)请在图②和图③中分别画出一个与△ABC相似,且互补全等的格点三角形,并写出相应的相似比k(△ABC与△A′B′C′之比) 

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)直接写出不等式![]() 的解集;
的解集;
(3)若点A关于y轴的对称点为C,问是否在x轴下方存在一点D,使以点A、B、C、D为顶点的四边形是平行四边形.若存在,直接写出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新年晚会,是我们最欢乐的时候.会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形,如图所示.
(1)数一下每一个多面体具有的顶点数![]() 、棱数
、棱数![]() 和面数
和面数![]() .并且把结果记入表中.
.并且把结果记入表中.
多面体 | 顶点数 | 面数 | 棱数 |
正四面体 | 4 | 4 | 6 |
正方体 | |||
正八面体 | |||
正十二面体 | |||
正二十面体 | 12 | 20 | 30 |
(2)观察表中数据,猜想多面体的顶点数![]() 、棱数
、棱数![]() 和面数
和面数![]() 之间的关系.
之间的关系.
(3)伟大的数学家欧拉(Euler,1707-1783)证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数![]() =196,棱数
=196,棱数![]() =294.请你用欧拉公式求这个多面体的面数.
=294.请你用欧拉公式求这个多面体的面数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个十字形花坛铺上了草皮,四个角没有植草的部分都是正方形.
(1)此花坛草地的面积,可以用代数式表示为 ;
(2)若a=12米,b=8米,c=2米,此花坛草地的面积是多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB,OM,ON是
,OB,OM,ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当射线OB绕点O在
当射线OB绕点O在![]() 内旋转时,
内旋转时,![]() ______度
______度![]()
![]() 也是
也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当
,当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 绕O点以每秒
绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() :
:![]() :3,求t的值.
:3,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
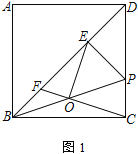
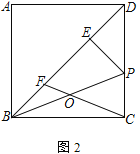
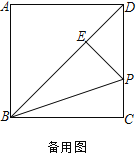
【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.
(1)O为BP的中点,连接CO并延长交BD于点F
①如图1,连接OE,求证:OE⊥OC;
②如图2,若![]() ,求DP的长;
,求DP的长;
(2)![]() =___________
=___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com