解:(1)把x=1代入x
2+2x+3中,得:1
2+2+3=6;
若x=2,则这个代数式的值为2
2+2×2+3=11;
可见,这个代数式的值因x的取值不同而变化;
(2)根据题意可得:
x
2+2x+3=(x
2+2x+1)+2=(x+1)
2+2,
∵(x+1)
2是非负数,
∴这个代数式x
2+2x+3的最小值是2,相应的x的值是-1;
(3)∵-x
2+14x+10=(x-7)
2-59,
∴-x
2+14x+10的最小值是-59,相应的x的值是7;
(4)根据题意得:
∴2x
2-12x+1=(x-3)
2-8

,
∴代数式2x
2-12x+1的最小值是-8

,相应的x的值是3;
(5)∵
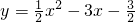
,
∴y=

(x-3)
2-6,
∵x的值在数1~4(包含1和4)之间变化,
∴这时y的变化范围是:-6≤y≤-4.
故答案为:6,11,变化;故答案为:-2,1.
分析:(1)把x=1和x=2分别代入代数式x
2+2x+3中,再进行计算即可得出答案,再比较数值的变化情况即可;
(2)根据非负数的性质即可得出答案;
(3)先把给出的式子化成完全平方的形式,再根据非负数的性质即可得出答案;
(4)根据完全平方公式把给出的式子进行整理,即可得出答案;
(5)先把代数式化成完全平方的形式,再根据非负数的性质以及x的取值范围即可得出答案.
点评:此题考查了因式分解的应用,用到的知识点是完全平方公式,非负数的性质,解题的关键是把给出的式子化成完全平方的性质进行解答.

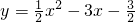 ,且x的值在数1~4(包含1和4)之间变化,求这时y的变化范围.
,且x的值在数1~4(包含1和4)之间变化,求这时y的变化范围. ,
, ,相应的x的值是3;
,相应的x的值是3;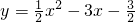 ,
, (x-3)2-6,
(x-3)2-6,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案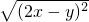 =1,
=1,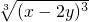 =-1,求
=-1,求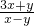 的值.
的值.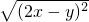 =1,得(2x-y)2=1,2x-y=1第一步
=1,得(2x-y)2=1,2x-y=1第一步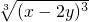 =-1,得x-2y=-1…第二步
=-1,得x-2y=-1…第二步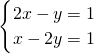 ,解得
,解得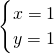 …第三步
…第三步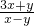 中,得
中,得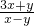 =0 …第四步
=0 …第四步