
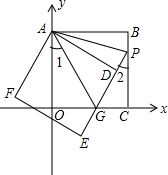
 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.分析 (1)由AO=AD,AG=AG,根据斜边和一条直角边对应相等的两个直角三角形全等,判断出△AOG≌△ADG即可.
(2)首先根据三角形全等的判定方法,判断出△ADP≌△ABP,再结合△AOG≌△ADG,可得∠DAP=∠BAP,∠1=∠DAG;然后根据∠1+∠DAG+∠DAP+∠BAP=90°,求出∠PAG的度数;最后判断出线段OG、PG、BP之间的数量关系即可.
(3)首先根据△AOG≌△ADG,判断出∠AGO=∠AGD;然后根据∠1+∠AGO=90°,∠2+∠PGC=90°,判断出当∠1=∠2时,∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,求出∠1=∠2=30°;最后确定出P、G两点坐标,即可判断出直线PE的解析式.
(4)根据题意,分两种情况:①当点M在x轴的负半轴上时;②当点M在EP的延长线上时;根据以M、A、G为顶点的三角形是等腰三角形,求出M点坐标是多少即可.
解答 (1)证明:在Rt△AOG和Rt△ADG中,
$\left\{\begin{array}{l}{AO=AD}\\{AG=AG}\end{array}\right.$(HL)
∴△AOG≌△ADG.
(2)解:在Rt△ADP和Rt△ABP中,
$\left\{\begin{array}{l}{AD=AB}\\{AP=AP}\end{array}\right.$
∴△ADP≌△ABP,
则∠DAP=∠BAP;
∵△AOG≌△ADG,
∴∠1=∠DAG;
又∵∠1+∠DAG+∠DAP+∠BAP=90°,
∴2∠DAG+2∠DAP=90°,
∴∠DAG+∠DAP=45°,
∵∠PAG=∠DAG+∠DAP,
∴∠PAG=45°;
∵△AOG≌△ADG,
∴DG=OG,
∵△ADP≌△ABP,
∴DP=BP,
∴PG=DG+DP=OG+BP.
(3)解:∵△AOG≌△ADG,
∴∠AGO=∠AGD,
又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,
∴∠AGO=∠PGC,
又∵∠AGO=∠AGD,
∴∠AGO=∠AGD=∠PGC,
又∵∠AGO+∠AGD+∠PGC=180°,
∴∠AGO=∠AGD=∠PGC=180°÷3=60°,
∴∠1=∠2=90°-60°=30°;
在Rt△AOG中,
∵AO=3,
∴OG=AOtan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴G点坐标为($\sqrt{3}$,0),CG=3-$\sqrt{3}$,
在Rt△PCG中,PC=$\frac{CG}{tan30°}$=$\frac{3-\sqrt{3}}{\frac{\sqrt{3}}{3}}$=3($\sqrt{3}$-1),
∴P点坐标为:(3,3$\sqrt{3}$-3 ),
设直线PE的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{\sqrt{3}k+b=0}\\{3k+b=3\sqrt{3}-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=-3}\end{array}\right.$,
∴直线PE的解析式为y=$\sqrt{3}$x-3.
(4)①如图1,当点M在x轴的负半轴上时, ,
,
∵AG=MG,点A坐标为(0,3),
∴点M坐标为(0,-3).
②如图2,当点M在EP的延长线上时, ,
,
由(3),可得∠AGO=∠PGC=60°,
∴EP与AB的交点M,满足AG=MG,
∵A点的横坐标是0,G点横坐标为$\sqrt{3}$,
∴M的横坐标是2$\sqrt{3}$,纵坐标是3,
∴点M坐标为(2$\sqrt{3}$,3).
综上,可得
点M坐标为(0,-3)或(2$\sqrt{3}$,3).
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,以及直线的解析式的求法,要熟练掌握.
(3)此题还考查了等腰三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
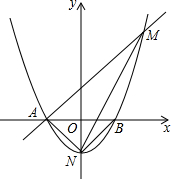 如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).
如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )
如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )| A. | 36cm2 | B. | 48cm2 | C. | 64cm2 | D. | 72cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.
如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.
如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8cm | B. | 5$\sqrt{2}$cm | C. | 5.5cm | D. | 1cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com