
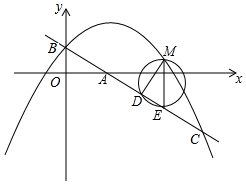
 在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).分析 (1)利用待定系数法求抛物线的解析式;
(2)如图1,A与E重合,根据直线y=-$\frac{3}{4}$x+1求得与x轴交点坐标可得OA的长,由勾股定理得AB的长,利用等角的三角函数得:sin∠ABO=$\frac{OA}{AB}=\frac{4}{5}$,cos∠ABO=$\frac{OB}{AB}$=$\frac{3}{5}$,则可得DE和DM的长,根据M的横坐标代入抛物线的解析式可得纵坐标,即ME的长,相加得△DEM的周长;
(3)由旋转可知:O1A1⊥x轴,O1B1⊥y轴,设点A1的横坐标为x,则点B1的横坐标为x+1,所以点O1,A1不可能同时落在抛物线上,分以下两种情况:
①如图2,当点O1,B1同时落在抛物线上时,根据点O1,B1的纵坐标相等列方程可得结论;
②如图3,当点A1,B1同时落在抛物线上时,根据点B1的纵坐标比点A1的纵坐标大$\frac{4}{3}$,列方程可得结论.
解答 解:(1)∵直线y=-$\frac{3}{4}$x+1交y轴于点B,
∴B(0,1),
∵抛物线y=-$\frac{1}{2}$x2+bx+c经过点B和点C(4,-2).
∴$\left\{\begin{array}{l}{c=1}\\{-8+4b+c=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{5}{4}}\\{c=1}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+$\frac{5}{4}$x+1;
(2)如图1,∵直线y=-$\frac{3}{4}$x+1交x轴于点A,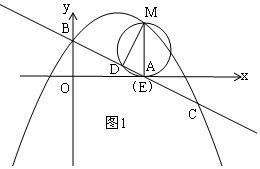
当y=0时,-$\frac{3}{4}$x+1=0,
x=$\frac{4}{3}$,
∴A($\frac{4}{3}$,0),
∴OA=$\frac{4}{3}$,
在Rt△AOB中,
∵OB=1,
∴AB=$\frac{5}{3}$,
∴sin∠ABO=$\frac{OA}{AB}=\frac{4}{5}$,cos∠ABO=$\frac{OB}{AB}$=$\frac{3}{5}$,
∵ME∥x轴,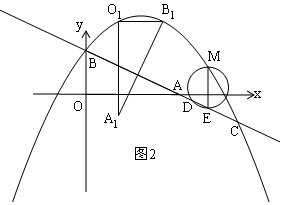
∴∠DEM=∠ABO,
∵以ME为直径的圆交直线BC于另一点D,
∴∠EDM=90°,
∴DE=ME•cos∠DEM=$\frac{3}{5}$ME,
DM=ME•sin∠DEM=$\frac{4}{5}$ME,
当点E在x轴上时,E和A重合,则m=OA=$\frac{4}{3}$,
当x=$\frac{4}{3}$时,y=-$\frac{1}{2}$×$(\frac{4}{3})^{2}$+$\frac{5}{4}$×$\frac{4}{3}$+1=$\frac{16}{9}$;
∴ME=$\frac{16}{9}$,
∴DE=$\frac{3}{5}×\frac{16}{9}$=$\frac{16}{15}$,DM=$\frac{4}{5}×\frac{16}{9}$=$\frac{64}{45}$,
∴△DEM的周长=DE+DM+ME=$\frac{16}{15}$+$\frac{64}{45}$+$\frac{16}{9}$=$\frac{64}{15}$;
(3)由旋转可知:O1A1⊥x轴,O1B1⊥y轴,设点A1的横坐标为x,则点B1的横坐标为x+1,
∵O1A1⊥x轴,
∴点O1,A1不可能同时落在抛物线上,分以下两种情况:
①如图2,当点O1,B1同时落在抛物线上时,
点O1,B1的纵坐标相等,
∴-$\frac{1}{2}{x}^{2}+\frac{5}{4}x+1$=-$\frac{1}{2}$(x+1)2+$\frac{5}{4}$(x+1)+1,
解得:x=$\frac{3}{4}$,
此时点A1的坐标为($\frac{3}{4}$,$\frac{31}{96}$),
②如图3,当点A1,B1同时落在抛物线上时,
点B1的纵坐标比点A1的纵坐标大$\frac{4}{3}$,
-$\frac{1}{2}{x}^{2}+\frac{5}{4}x+1+\frac{4}{3}$=-$\frac{1}{2}$(x+1)2+$\frac{5}{4}$(x+1)+1,
解得:x=-$\frac{7}{12}$,
此时A1(-$\frac{7}{12}$,$\frac{29}{288}$),
综上所述,点A1($\frac{3}{4}$,$\frac{31}{96}$)或(-$\frac{7}{12}$,$\frac{29}{288}$).
点评 本题是二次函数与圆的综合题,考查了利用待定系数法求二次函数的解析式、圆周角定理、三角函数、与坐标轴的交点,第三问有难度,准确地画出图形是关键,与方程相结合,找等量关系列方程解决问题,并采用了分类讨论思想,不要丢解.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:填空题
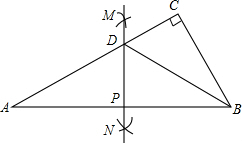 如图,△ABC中,∠C=90°,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.若DC=3,BC=4,则AB=4$\sqrt{5}$.
如图,△ABC中,∠C=90°,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.若DC=3,BC=4,则AB=4$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=±3 | B. | a=3 | C. | a=-3 | D. | a=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )
为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )| A. | $\left\{\begin{array}{l}{x+45y=180}\\{65x+y=10100}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{45x+y=180}\\{x+65y=10100}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=180}\\{65x+45y=10100}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{45x+65y=10100}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/辆) | a | b |
| 年均载客量(万人/年/辆) | 60 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{k}{a}$=x1-x2 | B. | $\frac{k}{a}$=x2-x1 | C. | $\frac{k}{a}$=x1+x2 | D. | $\frac{k}{a}$=-(x1+x2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com