
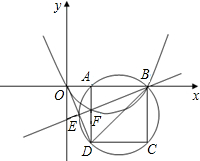
 如图,在平面直角坐标系中,已知点A(m,0)(0<m<$\sqrt{2}$),B(2$\sqrt{2}$,0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆的交点,连接BE与AD相交于点F.
如图,在平面直角坐标系中,已知点A(m,0)(0<m<$\sqrt{2}$),B(2$\sqrt{2}$,0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆的交点,连接BE与AD相交于点F.分析 (1)本题可通过全等三角形来证简单的线段相等,三角形ABF和ADO中,根据圆周角定理可得出∠ABF=∠ADO,已知了一组直角和AB=AD,因此两三角形全等,即可得出BF=OD的结论;
(2)如果G是三角形BDO的外心,根据三角形外心定义可知BE必垂直平分OD,因此三角形BOD是等腰三角形.在等腰直角三角形ABD中,BD=BO=2$\sqrt{2}$,AB=OB-OA=2$\sqrt{2}$+m,因此可根据AB、BD的比例关系求出m的值,即可得出OA的长,而在(1)得出的全等三角形中,可得出OA=FG,据此可求出F点坐标.已知B、F、O三点坐标,可用待定系数法求出抛物线的解析式;
(3)当直线BE与y轴相交于G,向上平移直线BE使平移后的直线经过原点O,由图象知,在平移前直线BE与新图象有1个公共点,平移到经过点O时与新图象有3个公共点,并且0<t<OG,利用已知条件求出OG的长即可求出t的取值范围;当直线BE向上平移至于抛物线相切后再向上平移时,直线BE与图象的交点又变为两个,设相切时直线BE的解析式为y=($\sqrt{2}$-1)x+b,求出方程组的解,进而求出t的取值范围.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠DAO=90°
在△ABF和△ADO中
$\left\{\begin{array}{l}{∠ABF=∠ADO}\\{AB=AD}\\{∠BAF=∠DAO}\end{array}\right.$
∴△ABF≌△ADO(ASA),
∴BF=DO;
(2)∵A(m,0),B(2$\sqrt{2}$,0),
∴AO=m,BO=2$\sqrt{2}$,AB=2$\sqrt{2}$-m,
∵$\widehat{AE}$=$\widehat{DE}$,
∴∠EBO=∠EBD,
∵∠DAB=90°,
∴BD为直径∴∠BEO=∠BED=90°,
又∵BE=BE,
∴△BEO≌△BED,
∴BD=BO=2$\sqrt{2}$,
在Rt△BCD中BD=$\sqrt{2}$AB,
∴2$\sqrt{2}$=$\sqrt{2}$(2$\sqrt{2}$-m),
∴m=2$\sqrt{2}$-2,
∵△ABF≌△ADO,
∴AF=AO=m=2$\sqrt{2}$-2,
∴F点的坐标为(2$\sqrt{2}$-2,2-2$\sqrt{2}$),
∵抛物线C经过O(0,0),B(2$\sqrt{2}$,0),
设C的解析式为y=ax(x-2$\sqrt{2}$),
将F(2$\sqrt{2}$-2,2-2$\sqrt{2}$)代入得:a=$\frac{1}{2}$,
∴抛物线l的解析式为y=$\frac{1}{2}$x2-$\sqrt{2}$x;
(3)①如图,设直线BE与y轴相交于G,向上平移直线BE使平移后的直线经过原点O,由图象知,在平移前直线BE与新图象有1个公共点,平移到经过点O时与新图象有3个公共点.
∴0<t<OG,
设直线BE的解析式为y=kx+m,将B(2$\sqrt{2}$,0),F(2$\sqrt{2}$-2,2-2$\sqrt{2}$)代入易求出:y=($\sqrt{2}$-1)x-4+2$\sqrt{2}$,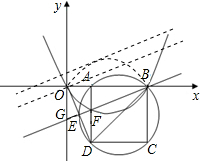
当x=0时,y=-4+2$\sqrt{2}$,
∴OG=4-2$\sqrt{2}$,
此时t的取值范围是:0<t<4-2$\sqrt{2}$.
②如图,当直线BE向上平移至于抛物线相切后再向上平移时,直线BE与图象的交点又变为两个,设相切时直线BE的解析式为y=($\sqrt{2}$-1)x+b,
则方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\sqrt{2}x}\\{y=(\sqrt{2}-1)x+b}\end{array}\right.$有一个解,
于是方程-$\frac{1}{2}$x2-$\sqrt{2}$x=($\sqrt{2}$-1)x+b有两个相等的实数根,
即△=0,解得b=$\frac{1}{2}$,
此时直线BE的解析式为y=($\sqrt{2}$-1)x+$\frac{1}{2}$,
直线BE与y轴的交点为(0,$\frac{1}{2}$),
∴OG=$\frac{1}{2}$+(4-2$\sqrt{2}$)=$\frac{9}{2}$-2$\sqrt{2}$,
∴此时t的取值范围是:t>$\frac{9}{2}$-2$\sqrt{2}$.
综上所述:t的取值范围为:0<t<4-2$\sqrt{2}$或t>$\frac{9}{2}$-2$\sqrt{2}$.
点评 本题考查了二次函数的性质,二次函数和圆的交点问题,以及正方形的性质和全等三角形的判定和全等三角形的性质,本题有一定的难度,综合性也比较强,有一定的新意,第3小问有些难度,有一定的能力要求,解这种题时需冷静地分析题意,找到切入点不会很难.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某报社为了解我市市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,其中有一个问题是:“您觉得雾霾天气对您哪方面的影响最大?”五个选项分别是:A.身体健康;B.出行;C.情绪不爽;D.工作学习;E.基本无影响,根据调查统计结果,绘制了如下三幅尚不完整的三种统计图、表:
某报社为了解我市市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,其中有一个问题是:“您觉得雾霾天气对您哪方面的影响最大?”五个选项分别是:A.身体健康;B.出行;C.情绪不爽;D.工作学习;E.基本无影响,根据调查统计结果,绘制了如下三幅尚不完整的三种统计图、表:| 雾霾天气对您哪方面的影响最大 | 百分比 |
| A. 身体健康 | m |
| B. 出行 | 15% |
| C.情绪不爽 | 10% |
| D. 工作学习 | n |
| E. 基本无影响 | 5% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的大小等于( )
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的大小等于( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com