Question

在Rt△ABC中，∠C=90°，∠A=30°，BC=2．若将此直角三角形的一条直角边BC或AC与x轴重合，使点A或点B刚好在反比例函数 （x＞0）的图象上时，设△ABC在第一象限部分的面积分别记做S₁、S₂（如图1、图2所示）D是斜边与y轴的交点，通过计算比较S₁、S₂的大小．

 

Answer 1

【答案】

S₁=S₂=6﹣

【解析】

试题分析：根据反比例函数的性质，可以得到点A和点B的坐标，分别计算出S₁，S₂的值，然后比较它们的大小．

解：如图1：∵∠C=90°，∠A=30°，BC=2，

∴AC=2，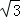

∵点A在y=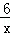上，

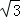∴A（，2），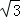

即OC=，

OB=2﹣，

OD=2﹣3，

∴S₁=（OD+AC）?OC，

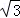=（2﹣3+2）×，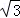

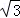=6﹣；

如图2：∵BC=2，∠A=30°，

∴点B的纵坐标是2，AC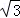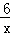=2，

∴=2，

解得x=3，

∴B（3，2），

∴AO=2﹣3，

∵，

∴，

∴OD=2﹣，

S₂=（OD+BC）?OC，

=（2﹣+2）×3，

=6﹣．

所以S₁=S₂．

考点：反比例函数综合题．

点评：本题考查的是反比例函数的综合题，根据反比例函数的性质，结合图形计算面积．