
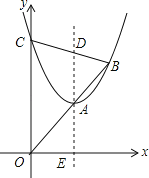
【题目】如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=![]() .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
【答案】![]() 或
或![]() .
.
【解析】
设A(2m,3m)、B(2n,3n),分点A在线段OB上及点B在线段OA上两种情况,由OC=2AD,利用相似三角形的性质可得出m、n间的关系,将A、B点坐标代入抛物线与抛物线对称轴x=2m联立方程组,解方程组即可求得c的值.
解:由tan∠AOE=![]() ,可设A、B点坐标分别为(2m,3m)、(2n,3n),
,可设A、B点坐标分别为(2m,3m)、(2n,3n),
∵AD∥OC,
∴∠ADB=∠OCB,∠DAB=∠COA,
∴△BAD∽△BOC.
①当点A在线段OB上时,如图1所示.
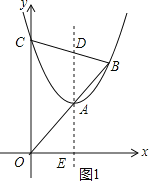
∵OC=2AD,
∴D点为线段BC的中点,
∵C(0,c),B(2n,3n),
∴D点横坐标为![]() =n,
=n,
由题意知A、D点均在抛物线的对称轴上,
∴n=2m,
∴B点坐标为(4m,6m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有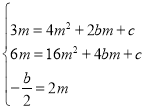 ,
,
解得:![]() ,或
,或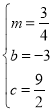 ,
,
∵c>0,
∴c=![]() ;
;
②当点B在线段OA上时,如图2所示.
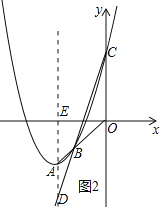
∵OC=2AD,
∴OB=2AB.
∵C(0,c),B(2n,3n),
∴D点横坐标为![]() ×2n=3n,
×2n=3n,
由题意知A、D点均在抛物线的对称轴上,
∴n=![]() m,
m,
∴B点坐标为(![]() m,2m),
m,2m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有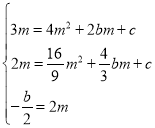 ,
,
解得:![]() ,或
,或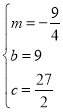 .
.
∵c>0,
∴c=![]() .
.
综上所述:c的值为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
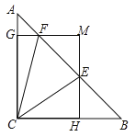
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
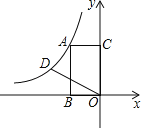
【题目】如图,矩形ABOC的顶点B、C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(﹣2,0).将线段OC绕点O逆时针旋转60°至线段OD,若反比例函数y=![]() (k≠0)的图象经过A、D两点,则k值为______.
(k≠0)的图象经过A、D两点,则k值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款新产品,通过市场调研后,按三种颜色受欢迎的程度分别对A颜色、B颜色、C颜色的产品在成本的基础上分别加价40%,50%,60%出售(三种颜色产品的成本一样),经过一个季度的经营后,发现C颜色产品的销量占总销量的40%,三种颜色产品的总利润率为51.5%,第二个季度,公司决定对A产品进行升级,升级后A产品的成本提高了25%,其销量提高了60%,利润率为原来的两倍;B产品的销量提高到与升级后的A产品的销量一样,C产品的销量比第一季度提高了50%,则第二个季度的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
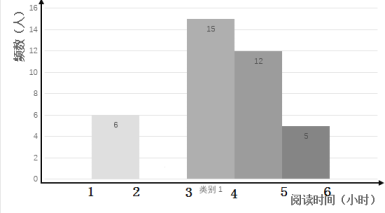
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
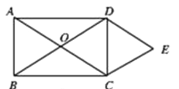
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上两动点,且
上两动点,且![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)试探究![]() 、
、![]() 、
、![]() 之间有何数量关系?说明理由.
之间有何数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
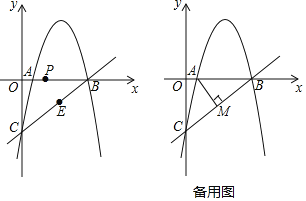
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com